Geology Reference
In-Depth Information
+ u/ t - T
2
u/ x
2
= 0 and attempt u(x,t) = sin (kx - t) once more. It is clear
from the even and odd derivative combinations in the differential equation that
our trigonometric functions will never cancel. This may have been anticipated
from Equation 1.44, which indicates that dissipation affects phase nontrivially.
As before, we instead attempt a complex substitution. The choice u(x,t) =
A exp i(kx-
t) leads to
l
2
= Tk
2
- i
, which is a “complex dispersion”
relation. So,
must be likewise complex; we consider the “complex frequency”
(k) =
r
(k) + i
i
(k)
(1.48)
Direct substitution now yields
l
(
r
2
-
i
2
+ i 2
i
) = Tk
2
- i
r
+ i
i
=
r
Tk
2
+
r
2
-
i
2
)= Tk
2
+
(
-i
r
). Next, taking real parts gives
l
(
i
,
i
whereas taking imaginary parts gives
l
2
r i
= -
r
or
i
= - / 2
l
.
As Equation 1.44 suggests, the “real dispersion relation”
l
(
r
2
-
i
2
)=
Tk
2
+
i
is affected by dissipation. The “imaginary frequency”
i
= - / 2
l
for our damped equation, is a constant independent of k, but in general this is
not so. If the attenuation is weak, with |
i
/
r
| << 1 and small, the real
dispersion relation can be approximated by the undamped result
l
r
2
= Tk
2
.
There are more wave properties to elaborate upon. First, observe that in all
of the equations considered so far, none contain variable coefficients, also
known as “nonuniformities,” “inhomogeneities” or “heterogeneities.” Certainly,
we can envision a problem where the lineal mass density
l
varies with x, and
the tension T varies with time. If these variations are weak, we can explicitly
write
l
( x)
2
u/ t
2
- T ( t)
2
u/ x
2
= 0 and expect that the “uniform plane
wave” result
l
r
2
= Tk
2
obtained earlier applies locally. That is, we
physically expect that
l
( x)
r
2
= T( t) k
2
holds to leading order, which can be
demonstrated by formal “WKB asymptotic methods.” The new dispersion
relation now describes a “slowly varying wavetrain.” For waves in dissipative
media, the “inhomogeneous dispersion relation” is
(k) =
r
(k,x,t) + i
i
(k,x,t)
(1.49)
where
r
(k,x,t) and
i
(k,x,t) may be obtained analytically, as we have done
here, or experimentally from laboratory results.
Classical wave theory is equation-based in that partial differential
equations are studied for engineering systems; for example, the physical model
l
2
u/ t
2
+ u/ t - T
2
u/ x
2
= 0 is derived and analyzed. If the consequences
of a model do not agree with experiment, another is proposed and its
consequences studied. This approach can be tedious, since the simplest
equations often elude convenient solution.




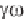



















































Search WWH ::

Custom Search