Geology Reference
In-Depth Information
lengths, it will lose its identity after a finite time in a dispersive medium.
Dispersion in
MWD
communications channels is undesirable, since information
packets must be periodically reassembled; fortunately, in mud pulse telemetry,
dispersion is much less a problem than is attenuation.
In time-dependent problems, wave properties
may
be proportional to e
i t
or
sin ( t+ ), where is a “phase angle,” with the “angular frequency” being
constant. Since cycles appear in 2 units of time, the time per cycle or
“period” is 2 / , and the number of cycles per unit time or “frequency” is given
by f = /2 . The units of frequency f are “Hertz” (Hz), where
1 Hz is 1 cycle
per second
, while the units of angular frequency are
radians per second
. If a
periodic dependence on space (x) exists, e.g., sin (kx- t), or sin k(x-ct) where k
is the “wavenumber” and c = /k is the “phase velocity,” the repetition length or
“wavelength” is = 2 /k = 2 c/ = c / ( /2 ) or = c/f (e.g., if c = 4,800 ft/sec
and f = 12 Hz, then = 400 ft). Once the dispersion relation for a system is
known, either analytically or experimentally, the relationship between k and is
uniquely defined; in other words, when k is specified, can be computed, and
vice-versa. As we will show in Chapter 2,
the dispersion relation contains the
entire physical description of the wave propagation.
Two measures of wave speed are considered by physicists, acousticians,
electrical engineers and others, the “phase velocity” C
p
cited above and the
“group velocity” C
g
,
C
p
=
/k
(1.46)
C
g
= / k (1.47)
For the classical equation
l
2
u/ t
2
- T
2
u/ x
2
= 0, both phase and group
velocities happen to be identical - this is true of nondispersive systems. For
l
2
u/ t
2
+ u - T
2
u/ x
2
= 0, though, phase and group velocities differ.
The distinction between phase and group velocities was discovered by physicists
at the turn of the twentieth century. It turns out that “wave energy” (among
other quantities of physical interest, such as “wave momentum” and “wave
action”) propagates with group velocity in linear systems. Phase velocity, in the
grand scheme of Nature, is unimportant kinematically and dynamically.
Energy-based arguments play an important role in many practical problems. In
drillstring vibrations, for instance, severe downhole lateral oscillations cause
catastrophic failures and twistoffs near the neutral point. Yet, they
cannot
be
detected from the surface, even in vertical wells where borehole wall damping is
insignificant. This paradox is easily explained using group velocity arguments
in Chapter 4 and recommendations for danger avoidance are offered.
In the foregoing examples, the dispersion relations obtained were
real
, as
opposed to
complex
. Let us now consider the damped wave equation
l
2
u/ t
2




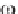

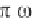




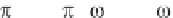




















Search WWH ::

Custom Search