Geology Reference
In-Depth Information
r
/ k E/ x = {2
i
- d
2 r
(k)/dk
2
k/ x} E(x) (10.19)
To determine E(x), Equation 10.18 (which is quadratic in k
1/2
) is first solved to
give an algebraic expression for k, that is in turn used to evaluate Equation
10.19. Then, the resulting equation first-order ordinary differential equation for
E(x) with variable coefficients can be integrated using any number of
elementary numerical schemes to provide the solution for E(x).
Properties following a ray are also easily obtained. In the above paragraph,
we obtained an expression for k from the quadratic formula. This is used to
evaluate
r
kk
(k) in Equation 10.17, so that a differential equation “dk
x
/dt = …”
for changes in k
x
along a ray is available with coefficients that depend on k.
This couples to the energy Equation 10.13 for d(log
e
E)/dt. An equation
describing changes in k is required. This is derived by carrying out the
differentiation specified in Equation 10.16, that is,
k/ t +
r
(k,x)/ x = k/ t +
r
k
(k,x) k/ x +
r
x
(k,x) = 0, which implies that dk/dt = k/ t +
r
k
(k,x)
k/ x = -
r
x
(k,x). In summary, we have the three equations dk/dt = -
r
x
(k,x),
dk
x
/dt = -
r
kk
(k) k
x
2
and d(log
e
E) /dt = {2
i
- d
2 r
(k)/dk
2
k
x
} for the three
unknowns k, k
x
and E which are integrated assuming suitable initial conditions.
Again, in heterogeneous problems, the rays in the x-t plane are curved and not
straight because the right side to dk/dt = -
r
x
(k,x) is no longer zero. That is, k
in not constant along a ray and the slope dx/dt =
r
k
(k,x) is variable. With
slight modification, this discussion applies to waves besides Stoneley waves.
10.2.3 Permeability prediction from energy considerations.
There are two methods to deduce formation permeability from Stoneley
wave data, the first via energy considerations and the second from phase
measurements. We consider the former in the section. To do this, we examine
the “total energy” contained within a waveform as opposed to the energy density
distribution along the length of a wave packet. Let us define the total wave
energy (t) following a wave packet, with E(x,t) being the energy density, x
1
(t)
and x
2
(t) representing two ray trajectories to be defined, and finally, x and t
denoting propagation coordinate and time, that is, set
x
2
(t)
(t) =
E(x,t) dx
(10.20)
x
1
(t)
The rate of change in total energy is obtained by taking the time derivative of
the above integral, making use of Liebnitz' s rule for differentiating variable
limits. We have, straightforwardly,




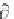


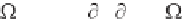










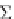









Search WWH ::

Custom Search