Geology Reference
In-Depth Information
To do this, we recognize that “k” physically represents the number of
waves per unit length, while “
r
” represents the number of oscillations per unit
time. If we consider the control volume (or more precisely, length) between two
fixed points A and B, it is clear that any increases in the number of wave crests
in time must be balanced the flux of frequency, that is, by frequency differences
measured at the endpoints. Therefore, “wave crest conservation” requires that
k/ t +
r
(k)/ x = 0 (10.16)
We now carry out the spatial derivation in Equation 10.16 using the chain rule
of calculus, at the same time introducing the convenient notation k
x
= k/ x.
This yields k
x
/ t +
r
(k)/ k
r
kk
(k)k
x
2
= 0, that is, along a ray,
k
x
/ x +
r
(k)/ k
r
kk
(k)k
x
2
< 0
dk
x
/dt =
k
x
/ t +
k
x
/ x = -
(10.17)
where we have invoked Equation 10.15. Thus, as the wave travels over large
distances, the negative value of k/ x at the front of the wave will become more
negative, leading to increasing amplification. At the same time, the positive
value of k/ x at the back of the wave will become less positive, thus slowing
the rate of decay, although it decays nonetheless. The central portion of the
wave, consistently with the synthetic seismogram of Figure 10.3, is in a sense
unaffected because k/ x 0 by virtue of the centered frequency excitation
provided by the Kelley source. These observations explain
why
the Stoneley
waveforms in Figure 10.3 behave the way they do. Finally, note that dk/dt = 0
along a ray dx/dt =
r
(k)/ k from Equation 10.16. The first equation states
that the wavenumber is constant along a ray in homogeneous media, so that the
dx/dt, which thus depends on k only, is likewise constant along a ray. This
constancy proves that rays (drawn in x-t coordinates) in homogeneous media are
straight and not curved. This, however, is not the case for waves in
heterogeneous media, e.g., when V or , or both, vary with x.
10.2.2 Dynamically steady Stoneley waves in heterogeneous
media.
There will be wellbore situations where the seven parameters cited earlier
are not constant but vary slowly in the propagation direction “x.” For Stoneley
wave motions that are dynamically steady, e.g., due to continuously operating
sources, it is possible to integrate the kinematic wave equations even when
variable V = V(x) and = (x) functions are specified. In this limit, the
frequency from Equation 10.16 must be a constant
0
of the problem, that is,
V(x)k - (x)k
1/2
=
0
(10.18)
which will not depend on the energy density E in linear problems. To find the
corresponding field solution for energy density, we specialize Equation 10.12 to
steady flow and obtain the following equation for E(x) -








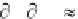













Search WWH ::

Custom Search