Geology Reference
In-Depth Information
u
n
"(t) + c
2
( n/L)
2
u
n
(t) = f
n
(t) (1.32)
Now, using Equation 1.28, our initial conditions can be written as u(x,0) = (x)
=
u
n
(0) sin nx/L =
n
sin nx/L and u
t
(x,0) =
(x) =
du
n
(0)/dt sin
nx/L =
n
sin nx/L where we have designated
u
n
(0) =
n
(1.33)
and
du
n
(0)/dt =
n
(1.34)
As in the previous example,
n
and
n
are known from Fourier expansions (see
Equations 1.24 to 1.26). This provides the initial conditions needed to integrate
Equation 1.32. If spatial variations in f(x,t) are rapid, numerous terms are
required for adequate spatial resolution. This is the case with concentrated
“delta function” loads, for which alternative solution methods are given later.
1.3.3 Example 1-5. Alternative boundary conditions.
We consider anticipated changes for other boundary condition classes. If
we had posed the derivative model u
x
(0,t) = u
x
(L,t) = 0, the solution would take
the form u(x,t) cos n x/L, with n = 0, 1, 2, 3, ..., so that u
x
(x,t) sin n x/L
vanishes at x = 0, L. And if we had posed the boundary conditions u(0,t) =
u
x
(L,t) = 0, we would have taken u(x,t) sin n x/L, which satisfies u(0,t) = 0.
Then, u
x
(x,t) cos n x/L leads to u
x
(L,t) cos n = 0; hence, n = 1/2, 3/2, 5/2,
and so on. Similar remarks apply to the problem requiring u
x
(0,t) = u(L,t) = 0.
From these examples, we observe recurring types of functions and
operations. The functions sin n x/L and cos n x/L which arose as a result of
our boundary condition classes and Fourier series manipulations are known as
“eigenfunctions,” “normal modes,” or “mode shapes.” The
n
in Equation 1.21
are known as “eigenvalues” or “characteristic values” of the system. If we write
the cos ( nct/L) function in Equation 1.23 in terms of a familiar cos t, we have
n
= nc/L, where the
n
represent the “natural frequencies” of the system.
1.3.4 Example 1-6. Mixed boundary conditions.
Eigenfunctions allow us to fit boundary conditions to series expansions.
We have dealt with sine and cosine series, but others are also used in
mathematics, e.g., series containing Bessel, Hankel, Hermite, Laguerrre and
Legendre functions. A given function may be expanded in any of these; the
nature of the boundary value problem, e.g., the host geometry, determines the
type used. Once the appropriate sequence of eigenfunctions is identified for a
problem, we can express any piecewise continuous function in the
corresponding series, since the coefficients depend only on integrated (not
differentiated) properties (see Equations 1.9 to 1.12).



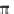





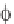
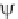






















Search WWH ::

Custom Search