Geology Reference
In-Depth Information
applying
initial conditions
. The substitutions u(x,0) = (x) =
u
n
(x,0) =
A
n
sin ( nx/L), together with Equations 1-11 and 1-12, lead to
A
n
= { 2 (x) sin n x/L dx}/L (1.25)
Similarly, u
t
(x,0) = (x) = u
n
(x,0)/ t = ( nc/L) B
n
sin ( nx/L) yields
B
n
= { 2 (x) sin n x/L dx}/( nc) (1.26)
Since A
n
and B
n
are known, the solution for u(x,t) is completely determined.
This formal construction does not necessarily produce a solution, e.g., if the
derived series diverges or if it is not differentiable. Here we have introduced the
use of eigenvalues and their corresponding eigenfunctions.
1.3.2 Example 1-4. String with distributed forces.
Now let us consider the inhomogeneous wave equation, with a non-zero
right side, namely,
2
u/ t
2
- c
2
2
u/ x
2
= f(x,t)
(1.27)
where the right side may represent the acceleration of a concentrated force, a
distributed force, or both. Again, we consider the boundary conditions u(0,t) = 0
and u(L,t) = 0, and the initial conditions u(x,0) =
(x) and u
t
(x,0) = (x).
Separation of variables again shows that sin nx/L is the appropriate function
satisfying boundary conditions. But since f(x,t) is nonzero and arbitrary, we
take a modified approach and write
u(x,t) = u
n
(t) sin nx/L (1.28)
To be consistent, we also expand the functions (x), (x) and f(x,t) in
similar series so that, for example, we obtain the Fourier series pair
f(x,t) =
f
n
(t) sin nx/L
(1.29a)
f
n
(t) = {2 f(x,t) sin n x/L dx}/L
(1.29b)
where t is a parameter. Likewise, we obtain,
(x) =
n
sin nx/L
(1.30a)
n
= { 2
(x) sin n x/L dx}/L
(1.30b)
(x) =
n
sin nx/L
(1.31a)
n
= { 2 (x) sin n x/L dx}/L (1.31b)
Substitution into Equation 1.27 leads to (sin nx/L){-c
2
( n/L)
2
u
n
(t) -
u
n
"(t) + f
n
(t)} = 0. This is satisfied if the coefficients within the { } brackets
vanish, that is, if the functions u
n
(t) obey the ordinary differential equation

















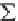







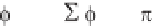



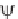
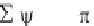














Search WWH ::

Custom Search