Geology Reference
In-Depth Information
s(x,y,z). But as we noted in our analysis of Equation 6.81 (or, u/ t + u u/ x =
0), shock formation and ray coalescence are in general possible, and some
additional information on the structure of the “small” right sides of Equations
6.118 and 6.119 is required. This is so if we recall that u/ t + u u/ x =
2
u/ x
2
and u/ t + u u/ x =
3
u/ x
3
have completely different solution
properties. Now where do we obtain information about these right-hand-sides?
The answer is clear if we recall that the classical eikonal equation shown in
Equation 6.99 is not the most general description for our seismic waves. In fact,
it turns out that the neglected high-order derivatives take a mathematical form
analogous to the
2
u/ x
2
in Burger' s equation, and that the exact structure of
the terms can be ascertained by extending one higher order our assumed high
frequency expansion. It is not necessary, though, to take this brute force
approach. As we had shown earlier, all of the information contained in the
eikonal equation is likewise embedded in the kinematic wave description,
including Fermat' s theorem, and more. Thus, the straightforward extension of
Equations 6.77 and 6.78 to two and three spatial dimensions provides high-order
partial differential equations that completely define the physics everywhere.
These equations, again, couple the effects of phase and amplitude.
Van Trier and Symes (1991) also noted that their analogues to Equations
6.118 and 6.119 may contain discontinuous gradients. Thus, they add
artificial
viscosity
to the governing equation, to render its solution unique, by using
upwind differencing in their numerical solution of the eikonal equation. This
introduces a “
2
u/ x
2
” type correction, and, as does Burger' s equation,
smooths out all shocks. The though, depends on details of the mesh, the
truncation error of the numerical approximation scheme used, and the details of
the programming and coding (see Dablain (1984) for a discussion of truncation
error forms used in seismics). It does
not
represent a true physical effect, based
on real attenuation and viscous diffusion, as Equations 6.77 and 6.78 would.
Thus, the upwinding yields results that may
appear
correct, but which in fact are
not. This same point is expressed in Chin (1993a), in the context of numerical
reservoir simulation, commenting on models where upwind differencing is used
in conjunction with true capillary pressure based diffusion to stabilize steep
saturation gradients. Similar concerns were also expressed in a paper by
Geoltrain and Brac (1993). These authors experienced difficulties with
traveltimes computed by finite differencing, noting that many of the observed
irregularities have no physical basis for the velocity models used. Their
problems, of course, arose because they solved an incorrect form of the eikonal
equation; the proper high-order amplitude model, or Equations 6.77 and 6.78
(appropriately modified to contain the heterogeneities of the velocity model),
should yield correct physical results.
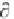


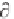

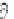
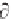












Search WWH ::

Custom Search