Geology Reference
In-Depth Information
6.4.1 Example 6-1. A simple model.
In Chapter 1, we considered two simple dissipative wave examples. In the
first, we studied the one-dimensional damped wave equation
2
u/ t
2
+ u/ t - T
2
u/ x
2
= 0 (6.40)
The substitution u(x,t) = A exp i(kx-
t) led to the complex dispersion relation
2
= Tk
2
- i
, which motivated us to assume a complex frequency
(k) =
r
(k) + i
i
(k). Direct substitution gave the real dispersion relation
(
r
2
-
i
2
)= Tk
2
+
(6.41)
i
and the imaginary frequency
i
= - /2 (6.42)
For weakly dissipative problems, Equation 6.41 can be approximated by the
nondissipative solution
r
2
= Tk
2
. But the more complete relation indicates
that propagation characteristics
are
affected by dissipation over large space and
time scales. The result
i
= - /2 is interesting from a different point of view.
The dissipation rate is a
constant
independent of k, and therefore, independent of
excitation frequency (this may not apply to specific applications).
6.4.2 Example 6-2. Another case history.
In this second review example, recall that we previously sought
dynamically steady
solutions to the damped equation
2
u/ t
2
+
u/ t - c
2
2
u/ x
2
= 0 (6.43)
satisfying u(0,t) = A cos
t. The result took the form
2
/c
4
)
1/4
cos{
½
arctan(- /
4
/c
4
+
2
u(x,t) = A exp { (
) + }}x
(6.44)
X cos { t + (
4
/c
4
+
2 2
/c
4
)
1/4
sin{
½
arctan(- / ) + }x}
Equation 6.44 is reminiscent of the u(x,t) A cos (t - x/c) for undamped
waves. The exact argument shows dissipation
does
affect the phase “ (t - x/c),”
and in addition, yields the expected exponential decrease in amplitude.
6.4.3 Example 6-3. Motivating damped wave study.
Let us now consider the three-dimensional wave equation with classical
damping, that is,
2
u/ t
2
+ u/ t - c
2
(
2
u/ x
2
+
2
u/ y
2
+
2
u/ z
2
) = 0 (6.45)
Following Example 6.1, the substitutions
u(x,y,z,t) = A exp i(k
x
x - k
y
y - k
z
z -
t) (6.46)
(k) =
r
(k) + i
i
(k) (6.47)
lead to







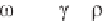


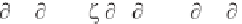

























Search WWH ::

Custom Search