Geology Reference
In-Depth Information
where ds represents the infinitesimal arc length given by
ds = (dx
2
+ dy
2
+ dz
2
)
(6.17a)
=
(dx/d )
2
+ (dy/d )
2
+ ( dz / d
)
2
}d
(6.17b)
Then, Equation 6.16 becomes
=
ray
(dx
2
+ dy
2
+ dz
2
) /c(x,y,z)
=
ray
c{x( ),y( ),z( )}
-1
(dx/d )
2
+ (dy/d )
2
+ ( dz / d
)
2
}d (6.18)
so that the
total time
T on each wave path is
1
T =
c{x( ),y( ),z( )}
-1
(dx/d )
2
+ (dy/d )
2
+ ( dz / d
)
2
}
1/2
d (6.19)
0
6.2.2 Calculus of variations.
“Calculus of variations” is the branch of advanced mathematics aimed at
solving maximal and minimal problems in continuum mechanics (Hildebrand,
1952; Gelfand and Fomin, 1963). From a standard argument, the x( ), y( ), and
z( ) values for a stationary value of
any
integral
1
F{ x (
),y( ), z( ),dx( )/d ,dy( )/d ,dz( )/d }d
(6.20)
0
must satisfy the variational “Euler equations” defined by
d{ F/ (dx/d )}/d - F/ x = 0 (6.21)
d{ F/ (dy/d )}/d - F/ y = 0 (6.22)
d{ F/ (dz/d )}/d - F/ z = 0 (6.23)
Let us consider Equation 6.21 in detail, in order to understand its
implications more fully. We now wish to explore the requirements for minimal
total travel time. If we set F equal to the travel time
definition
found in Equation
6.19, that is,
F = c { x (
),y( ),z( )}
-1
(dx/d )
2
+ (dy/d )
2
+ ( dz / d
)
2
}
1/2
(6.24)
we straightforwardly find that
F/ (dx/d ) = c
-1
(1/2){ }
-1/2
2 (dx/d ) = c
-1
{ }
-1/2
dx/d
(6.25)
and
F/ x = - c
-2
c
x
{ }
1/2
(6.26)
Then, Equation 6.21 becomes, using Equations 6.25 and 6.26,
d/d [ c
-1
{ }
-1/2
dx/d ] + c
-2
c
x
{ }
1/2
= 0
(6.27)
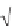





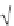

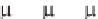
















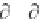







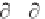









Search WWH ::

Custom Search