Geology Reference
In-Depth Information
the constant P
0
in Equation 6.2 has been replaced by a more general summation.
Since the expansion proceeds inversely with , it is a “high frequency”
assumption. Equation 6.4 is called a “ray series,” (x,y,z) is known as the
“phase function,” and the subscripted P
k
coefficients are the “amplitude
coefficients” of the series. When t is a given constant, the contours (x,y,z) = t
describe lines in space characterized by constant phase (refer to Equation 6.4
above). And because t = (k
x
x + k
y
y + k
z
z - constant)/ is the equation of the
planar wave front for the Equation 6.2, the moving surfaces of “constant phase”
t = (x,y,z) are called the “wave fronts” of Equation 6.4, and the orthogonal
trajectories of these surfaces are known as “rays” (a more precise definition is
given later). For Equation 6.2, we have (x,y,z) = (k
x
x + k
y
y + k
z
z)/ which, in
a single dimension, reduces to (x) = x/c. For a comprehensive treatment of
eikonal methods, the reader is referred to the topics by Cerveny and Ravindra
(1971) and Bleistein (1984).
6.1.3 Eikonal equation in nonuniform media.
We next consider a weakly inhomogeneous medium, retaining the isotropic
assumption, and in particular, Equation 6.1 with our constant c replaced by the
variable sound speed c(x,y,z). Substitution of Equation 6.4 in Equation 6.1
shows that, to leading order,
( / x)
2
+ ( / y)
2
+ ( / z)
2
= 1/c(x,y,z)
2
(6.5)
which is analogous to Equation 6.3, although not quite the same. The solution
to Equation 6.4, therefore, requires that Equation 6.5 in turn be solved. Equation
6.5 is known as the “eikonal equation,” and it is the nonlinear first-order partial
differential equation governing (x,y,z).
6.1.4 Continuing the series.
To obtain formulas governing and P
k
in the ray series of Equation 6.4, we
substitute Equation 6.4 into Equation 6.1 with our variable c(x,y,z), and carry
out all required expansions. Since the result must hold for any value of , the
coefficient of each power of must vanish. Equation 6.5 for the phase function
is obtained as the very first equation in this procedure, and it describes wave
kinematics only. To the next order, the “transport equation” governing the
amplitude function P
0
is obtained; it contains, in addition to P
0
, the effects of
propagation speeds, expressed in terms of functionals of
and its derivatives.
6.1.5 Integrating the eikonal equation.
In Chapter 1, a general solution method for first-order partial differential
equations was developed (see Equation 1.181, and Equations 1.210 to 1.218).
We will use it to integrate the eikonal equation. It will be convenient to
rearrange Equation 6.5 in the form

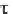


















Search WWH ::

Custom Search