Geology Reference
In-Depth Information
Equation 4.3.6, describing
r
, is known as the “real dispersion relation”
because it describes the
dispersive characteristics
of a propagating sinusoidal
wave exp{i(kx-
r
t)}. If we solve for the
phase velocity
C
p
=
r
(k)/k, it is clear
that waves having different wavelengths travel or
disperse
at different speeds.
This is in contrast to our experience with the second-order wave equation, where
the propagation speed is a fixed constant for all waves regardless of form. A
wave is “nondispersive” if all waves travel with the same identical speed;
otherwise, it is “dispersive.” Equation 4.3.7 describes the “imaginary
frequency”
i
. It is important to note that, unlike many examples in elementary
physics, a nonzero
i
function
can
appear even when purely attenuative effects
such as viscous dissipation are ignored. This is basically due to wave interaction
with an inhomogeneous medium, in this case, axial variations in axial force.
Again, in the present case, Equation 4.3.7 expresses the energy gained or
lost due to interactions with (variable properties in) the medium, namely, N(x,t).
Such interactions, consistently with the literature, occur through “radiation
stresses.” Sloping beaches, for example, introduce heterogeneities that affect
the dynamics of shallow water waves; they play important roles in wave
breaking. Now, since the drillstring is compressive at the bit and tensile at the
surface, it follows that
N/ x < 0, as a wave propagates up the drillstring in the
direction of increasing x. Thus, the imaginary frequency
i
in Equation 4.3.7 is
negative, indicating that any wave that propagates to the surface will damp on
account of interaction with the background strain field alone. This damping
will, of course, be enhanced by the effects of true viscous dissipation.
To determine the kinematics of the wave propagation, let us take partial
derivatives of Equation 4.3.6 with respect to k, leading to
r
/ k = 4 EI k
3
- 2Nk
2 A
(4.3.8)
r
and hence
C
g
=
r
/ k = (4EI k
3
- 2Nk)/2 A
r
= (2EI k
3
- Nk)/ A
r
(4.3.9)
Again, in a linear system, the
group velocity
C
g
is the velocity with which
energy and momentum both propagate; in nonlinear systems, energy,
momentum, and wavenumber will generally travel at different speeds.
Doe s C
g
ever vanish identically? The answer is a definitive
no
: this would
require that k
2
= N/(2EI), so that the right hand side of Equation 4.3.6, namely,
EI k
4
- Nk
2
= - N
2
/(4EI) would be negative, which is impossible, since the left
side requires the opposite, with A
r
2
> 0. To prove that C
g
is always nonzero,
although
the group velocity turns out to be extremely small near the neutral
point,
let us consider (without loss of generality) a dynamically steady, plane,
monochromatic wave having the fixed frequency
r
=
0
> 0
(4.3.10)





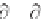















Search WWH ::

Custom Search