Geology Reference
In-Depth Information
our rock-bit interface with a well characterized wave because the primary effect
of elastic response is to distort the incident waveform.
For simplicity, we will consider an idealized rectangular displacement
pulse, and determine the nature of the reflected signal. The complete solution
containing displacement, velocity and stress, again, is implicit in the results
given earlier by Equations 4.2.45 to 4.2.52. We will expand upon the details,
and obtain specialized formulas for the rectangular pulse, in the process
demonstrating the use of Laplace transforms. Again, let us start with the general
solution to the undamped wave equation,
u(x,t) = f(ct-x) + g(ct+x)
(4.2.128)
but consider the rock-bit interaction model
u(0,t) = - u(0,t)/ x (4.2.129)
Now, differentiation of Equation 4.2.128 with respect to x yields, at x = 0,
u(x,t)/ x |
x=0
= -f '(ct-x) + g'(ct+x) |
x=0
= -f '(ct) + g'(ct) (4.2.130)
Substitution of Equations 4.2.128 and 4.2.130 in Equation 4.2.129 leads to
{f(ct) + g(ct)} = -
{-f '(ct)+g'(ct)}
(4.2.131)
We introduce the dummy variable = ct, to obtain
f '( ) - ( / )f( ) = g'( ) + ( / )g( ) (4.2.132)
for x = 0. We now define the Laplace transforms needed to obtain exact closed
form solutions. Let us introduce
f
*
(s) =
exp{-s } f( ) d
(4.2.133)
g
*
(s) =
exp{-s } g( ) d
(4.2.134)
Assuming zero initial conditions (that is, dynamically steady conditions when
the effects of initial conditions have vanished) we have
(s - / ) f* = (s + / ) g* (4.2.135)
Now we can re-express the right side coefficient in Equation 4.2.135 as s + /
= s - / + 2 / , so that
f* = g* + 2( /
) (g*)/(s - /
)
(4.2.136)
For the inverted solution, we formally write
f( ) = g( ) + 2( /
)
L
-1
{g*(s)/(s - /
)}
(4.2.137)
where
L
-1
denotes the inverse transform operation. At this point, we specialize
our results to a single pulsed displacement incident wave having a rectangular
shape. In particular, we set






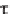

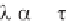







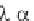




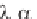
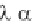
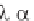

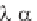









Search WWH ::

Custom Search