Geology Reference
In-Depth Information
dispersion relation c = /k =
f
(g, , s, m,k) or the eigenfunction (y). Sufficient
conditions for stability (
i
< 0), and specific calculated results are given in Chin
(1979) where the model is used to study flow stability over compliant surfaces.
3.5 Example 3-5. Problems in Hydrodynamic Stability
“Hydrodynamic stability” problems abound in nature. The best known
example is the flapping flag in wind. Ideally, a flag “should” remain flat and
undisturbed as uniform winds at either side flow by tangentially. But, of course,
this never occurs: the slightest perturbations set up instabilities that do not
decay. Here we introduce the subject of “shear flow instability” more generally,
whereby “shear flow” implies fluid that is flowing tangentially to a solid
surface. Previously we examined the behavior of the disturbance quantities u', v'
and p' to the parallel mean flow U(y) and its pressure P(y). We substituted
u(x,y,t) = U(y) + u'(x,y,t), v(x,y,t) = v'(x,y,t) and p(x,y,t) = P(y) + p'(x,y,t) into
complete
inviscid
equations and derived the governing Rayleigh equation. Then
we determined bounds on the complex eigenvalue. Although we did not derive
any explicit eigenvalue relations, these can be obtained straightforwardly for
specific velocity profiles (Chin, 1979).
A similar process applies to the complete
viscous
equation for
Newtonian
fluids; the analogous disturbances satisfy the
Orr-Sommerfeld
equation. Again,
streamfunctions proportional to (y) exp ik(x-ct) are assumed; the objective is
the eigenvalue relation c(k) = c
r
(k) + ic
i
(k) and its eigenfunction (y). Once
these are available, the solution of the complete initial value problem for general
wave-like disturbances to a particular flow U(y) is in principle known. If c
i
(k) >
0, the flow is said to be “unstable,” whereas it is “stable” if c
i
(k) < 0; otherwise,
the flow is “neutrally stable.” A comprehensive survey of the Orr-Sommerfeld
stability literature appears in Schlichting (1968).
3.5.1 Neutral stability diagrams.
Calculated hydrodynamic stability results are usually presented by means
of “stability diagrams.” A typical example is shown in Figure 3.5, derived for a
particular velocity profile U(y). On the horizontal axis is the dimensionless
“Reynolds number” R = U / for a “boundary layer flow,” where the length
scale is based on “boundary layer thickness” ( and represent density and
viscosity). On the vertical axis is the dimensionless product k , where k is the
wavenumber of the disturbance. The “neutral stability curve” shown,
determined from detailed eigenvalue analysis, delineates stable and unstable
regions of (k , U / ) space. Stability may be desirable in delaying the onset of
laminar-to-turbulent flow transition, while instability may be useful in
promoting rapid mixing. The “critical Reynolds number” is that number below
which all disturbances remain stable.






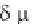













Search WWH ::

Custom Search