Geology Reference
In-Depth Information
p = - T
2
/ x
2
(3.68)
The complete unsteady
Bernoulli equation
(Lamb, 1945) is
/ t - gy - (u
2
+ v
2
)/2 + F(t)
p/ = -
(3.69)
where g is the acceleration due to gravity. If p is constant at the free surface,
e.g., equal to atmospheric pressure, then F(t) = 0. Since a mean flow does not
exist, the quadratic terms in Equation 3.69 are smaller than the linear ones, and
we have the approximation
p/
= -
/ t - gy
(3.70)
Equations 3.66, 3.68 and 3.70 imply the combined kinematical-dynamical free
surface condition
2
/ t
2
= ( T/
2
/ x
2
-g)
/ y
(3.71)
3.3.3 Problem solution.
We will solve Equation 3.65 for (x,y,t), subject to Equation 3.71 at the
unknown
free surface y = (x,t) and the condition that all motions cease at
infinity. As usual, we attempt separable solutions,
(x,y,t) = (y) e
i(kx-
t)
(3.72)
where k is a wavenumber and is the frequency (waveguide motions are
assumed in the x direction only). The function (y) provides the “cross-
structure” for the “modal” boundary value problem. Substitution of Equation
3.72 into
2
/ x
2
+
2
/ y
2
= 0 l e ads to "(y) - k
2
(y) = 0. The general
solution takes the form (y) = Ae
-ky
+ B e
+ky
where A and B are constants, but
only the contribution (y) = e
+ky
is meaningful since it gives decaying motions
at y = - . For this solution, we obtain '(y) = ke
+ky
(0) = 1, and '(0) = k.
Note that this modal problem, unlike our previous modal problem for
acoustical waveguides, is
not
a discrete eigenvalue problem. In fact, substitution
of Equation 3.72 in Equation 3.71 shows that
)
2
(y) = T/ (ik)
2
(-i
'(y) - g '(y)
(3.73)
)
2
(0) = T/ (ik)
2
(-i
'(0) - g '(0)
(3.74)
Consequently, we have the dispersion relation
2
= Tk
3
/ + gk
(3.75)
for any wave component with wavenumber k. Now, since (y) = e
+ky
is real, we
consider only the real part of Equation 3.72 and write
(x,y,t) = C e
+ky
cos (kx -
t)
(3.76)
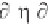



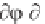
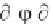




























Search WWH ::

Custom Search