Geology Reference
In-Depth Information
3.2.10 The velocity potential.
We take the opportunity to introduce the “velocity potential” while we are
dealing with fluid mechanics. This variable is important in simulating the
MWD acoustic fields produced by
negative pressure pulsers
. To facilitate the
discussion, we assume some familiarity with
vector calculus
(Hildebrand, 1948).
We make use of Equation 3.24 in the form
p = -
q
/ t. Now, we take the
m
curl
of each side, or
p = -
(
q
)/ t. But
p vanishes for any
m
function p(x,y,z,t), thus leaving the result (
q
)/ t = 0. Therefore,
q
is a
function of space; if it is zero at t = 0, it remains zero for all t > 0.
That
q
=
0
initially, and hence for all time, is well accepted in inviscid
fluid mechanics (that is, in flows absent of viscosity, as was assumed in this
section). This vanishing refers to the fact that (with special exceptions in
stratified flows and compressible flows with shockwaves) fluid elements in
inviscid media do not spin about their own axes while in translatory motion.
Note that the magnitudes of the elements of the
vorticity vector
=
q
are
proportional to the rotation rates of spinning particles. In the absence of spin,
we have
irrotational
flow; the non-rotating carts on a ferris wheel illustrate the
assumptions typical in acoustic analyses. An exception is sound propagation
through
shear flow
, a specialty important in jet engine design.
Again from vector calculus, any function
q
satisfying
q
=
0
, can be
represented as the
gradient
of a
potential
function (x,y,z,t), that is, as
q
=
.
Returning to scalar notation, the velocity components take the form
u =
/ x
(3.58a)
v =
/ y
(3.58b)
w =
/ z
(3.58c)
In summary, the result
q
=
0
allows us to express our velocities in the form
given by Equation 3.58a,b,c, that is, through a
single
function
and not three.
This is important to our deducing Equation 3.59 below.
For simplicity, consider one-dimensional wave motions satisfying
Equations 3.20 and 3.23, that is,
m
u/ t = - p/ x and '/ t +
m
u/ x = 0.
The first equation, together with u = / x, suggests that (p +
m
/ t)/ x = 0,
or p +
m
/ t = function of time only. This time function is purely constant if
the flow is steady far upstream; here, p = -
m
/ t applies to within an
insignificant constant. If we introduce a
compressibility
defined by ' =
m
p,
the equation
'/ t +
m
u/ x = 0 transforms into
p/ t +
u/ x = 0.
Substitution of p = -
/ t and u =
/ x yields
2
/ t
2
- (1/
m
)
2
/ x
2
= 0
m
or

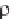



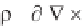




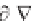










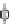


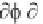
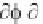







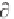

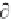
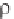





























Search WWH ::

Custom Search