Geology Reference
In-Depth Information
in Cartesian notation. To simplify
the discussion, we employ methods from vector calculus. We will take the
divergence of Equation 3.24 so that we obtain
where the velocity vector is
q
= u
i
+ v
j
+ w
k
o
q
/ t = -
2
p}, and
m
substitute the result
q
= - (1/
m
)
'/ t from Equation 3.25. This yields
2
'/ t
2
=
2
p
(3.26)
3.2.4 Three-dimensional wave equation.
At this point, the “constitutive laws” relating ' and p enter the derivation.
If the fluid is a gas, an equation of state relates the two, whereas a fluid analogy
to Hooke' s law = E applies to slightly compressible liquids (a detailed
development of the ideas appears later). In either case, the three-dimensional
wave equation
2
p/ t
2
- c
2
(
2
p/ x
2
+
2
p/ y
2
+
2
p/ z
2
) = 0 (3.27)
is obtained, where the constant c represents the speed of sound in the medium.
Again, Equation 3.27 assumes zero mean flow without physical damping.
3.2.5 Modal solution.
If we assume that our waveguide walls are infinitely rigid, Figure 3.2
suggests that wave energy must travel along the duct centerline, which we
define as the z axis. Therefore, the unknowns in Equations 3.20 to 3.22 may be
taken in the separable form
p(x,y,z,t) = P(x,y) exp i(
t -k
z
z) (3.28)
u(x,y,z,t) = U(x,y) exp i(
t -k
z
z)
(3.29)
v(x,y,z,t) = V(x,y) exp i(
t -k
z
z)
(3.30)
w(x,y,z,t) = W(x,y) exp i( t -k
z
z) (3.31)
In each of these product solutions, the “exp i( t-k
z
z)” represents a wave
propagating in the ± z direction, while the (x,y) reflects the “modal” or “cross-
structure” dependence of the solution. Then the assumptions
m
u/ t = - p/ x,
v/ t = - p/ y, and
m
w/ t = - p/ z in Equations 3.20 to 3.22 lead to
m
U(x,y) = - P
x
(x,y)/i
m
(3.32)
V(x,y) = - P
y
(x,y)/i
m
(3.33)
W(x,y) = P(x,y) k
z
/
m
(3.34)
while Equation 3.27 becomes
P
xx
+ P
yy
+ (
2
/c
2
- k
z
2
) P = 0
(3.35)

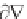
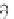


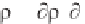
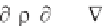







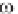



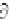

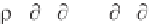


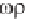









Search WWH ::

Custom Search