Geology Reference
In-Depth Information
k
z
/ t +
r
/ z = 0 (2.134)
Let us expand Equations 2-132 to 2-134 using the chain rule of calculus, so that
k
x
/ t +
r
kx
k
x
/ x +
r
ky
k
y
/ x +
r
kz
k
z
/ x=-
r
x
(2.135)
k
y
/ t +
r
kx
k
x
/ y +
r
ky
k
y
/ y +
r
kz
k
z
/ y=-
r
y
(2.136)
r
kx
r
ky
r
kz
k
z
/ z=-
r
z
k
z
/ t +
k
x
/ z +
k
y
/ z +
(2.137)
2.6.1 Wave irrotationality.
Recall our use of the phase function in Equations 2.84 and 2.85. In one
dimension, its motivation was furnished by wave solutions taking the form sin
(kx - t) or
sin
, where = - / t and k = / x (see Equations 2.8 and 2.9).
For slowly varying waves, we assume the existence of (x,y,z,t). Since
differentiation order can be interchanged, e.g.,
y
(x,y,z,t)/ x =
x
(x,y,z,t)/ y,
we have, setting k
x
=
x
(x,y,z,t) and k
y
=
y
(x,y,z,t), the result k
y
/ x = k
x
/ y.
In general, the “wave irrotationality” conditions
k
x
/ y = k
y
/ x
(2.138)
k
x
/ z = k
z
/ x (2.139)
k
y
/ z = k
z
/ y (2.140)
apply, using terminology adopted from fluid mechanics. Therefore, Equations
2.135 to 2.137 can be rewritten in the form
k
x
/ t +
r
kx
k
x
/ x +
r
ky
k
x
/ y+
r
kz
k
x
/ z = -
r
x
(2.141)
k
y
/ t +
r
kx
k
y
/ x +
r
ky
k
y
/ y+
r
kz
k
y
/ z = -
r
y
(2.142)
k
z
/ t +
r
kx
k
z
/ x +
r
ky
k
z
/ y +
r
kz
k
z
/ z = -
r
z
(2.143)
Since the k
x
(x,y,z,t) depends on four variables, namely, t, x, y, and z, its
total derivative is known from basic calculus as dk
x
= k
x
/ t dt + k
x
/ x dx +
k
x
/ y dy + k
x
/ z dz. Division by dt shows that
dk
x
/dt = k
x
/ t + dx/dt k
x
/ x + dy/dt k
x
/ y + dz/dt k
x
/ z
(2.144)
Similarly,
dk
y
/dt = k
y
/ t + dx/dt k
y
/ x + dy/dt k
y
/ y + dz/dt k
y
/ z
(2.145)
dk
z
/dt = k
z
/ t + dx/dt k
z
/ x + dy/dt k
z
/ y + dz/dt k
z
/ z
(2.146)












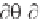






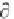


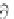
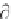







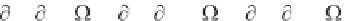


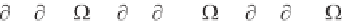
























Search WWH ::

Custom Search