Geology Reference
In-Depth Information
dx/dt =
r
k
(k,x,t)
(2.113)
Since dE/dt = E/ t +
r
k
(k,x,t) E/ x, Equation 2.111 becomes
dE/dt = E{2
i
+
r
t
(k,x,t)/
r
-
r
kx
(k,x,t) -
r
kk
(k,x,t) k/ x} (2.114)
The analysis for wave momentum, using Equation 2.105, proceeds along similar
lines. Since dM/dt = M/ t +
r
k
(k,x,t) M/ x, we analogously have
dM/dt = M{2
i
-
r
x
(k,x,t)/k
-
r
kx
(k,x,t) -
r
kk
(k,x,t) k/ x}
(2.115)
In Equations 2.114 and 2.115, the k/ x term requires numerical
differentiation across rays, using values computed by integration along rays.
The latter integrations can be performed using the previously suggested scheme
in Equations 2.26 and 2.27, namely,
k
f
= k
i
-
x
(k
i
,x
i
,t
i
)
t
(2.116)
x
f
= x
i
+
k
(k
i
,x
i
,t
i
)
t
(2.117)
For example, energy and momentum integrations proceed by writing
i
(k
i
,x
i
,t) +
r
t
(k
i
,x
i
,t)/
r
(k
i
,x
i
,t)
(E
f
- E
i
)/ t = E
i
{2
-
r
kx
(k
i
,x
i
,t) -
r
kk
(k
i
,x
i
,t) k
i
/ x}
(2.118)
(M
f
- M
i
)/ t = M
i
{2
i
(k
i
,x
i
,t) -
r
x
(k
i
,x
i
,t)/k
i
-
r
kx
(k
i
,x
i
,t) -
r
kk
(k
i
,x
i
,t) k
i
/ x}
(2.119)
and solving for E
f
and M
f
individually as in Equations 2.116 and 2.117 above.
More accurate numerical schemes are available in the literature, but Equations
2.118 and 2.119 illustrate the basic ideas.
2.5.5 Dynamically steady problems.
Often, constant frequency sources are used to create dynamically steady
wave patterns. This constancy provides an immediate integral of Equation
2.100; since k/ t = 0, we find that
r
(k,x) =
0
(2.120)
for the complex dispersion relation
(k,x) =
r
(k,x) + i
i
(k,x) (2.121)
For Equation 2.120 to apply, the excitation frequency
0
must be constant; there
must be no explicit dependence of (k,x) on time. Note that Equation 2.120
may be an algebraic equation, but it may also be transcendental. It may be
solved analytically or numerically for k(x).




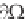


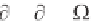
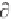
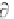

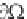


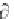







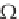




















Search WWH ::

Custom Search