From Riemann Manifolds to Riemann Manifolds - Map Projections: Cartographic Information Systems - page 22

Eckert II, all meridians and parallel circles are mapped as straight lines. The mapping equations
are given by

y = R 2 π
3

2 sign Φ,

√ 6 π Λ 4

4

2

x = R − 3sin | Φ | , − − 3sin | Φ |

sign Φ = +1 ∀ Φ ≥ 0

− 1 ∀ Φ< 0 .

(1.73)

End of Example.

We pose four problems. (i) Prove that the images of meridians and parallel circles are straight
lines. Prove the half length condition between the images of the central meridian and the pole,
respectively, and the equator. (ii) Derive the left Cauchy-Green deformation tensor. (iii) Solve
the left general eigenvalue-eigenvector problem. Prove the condition of an equiareal mapping
Λ 1 Λ 2 = 1. (iv) Prove that at { Λ =0 ,Φ =0 } the special pseudo-cylindrical projection is not an

isometry.

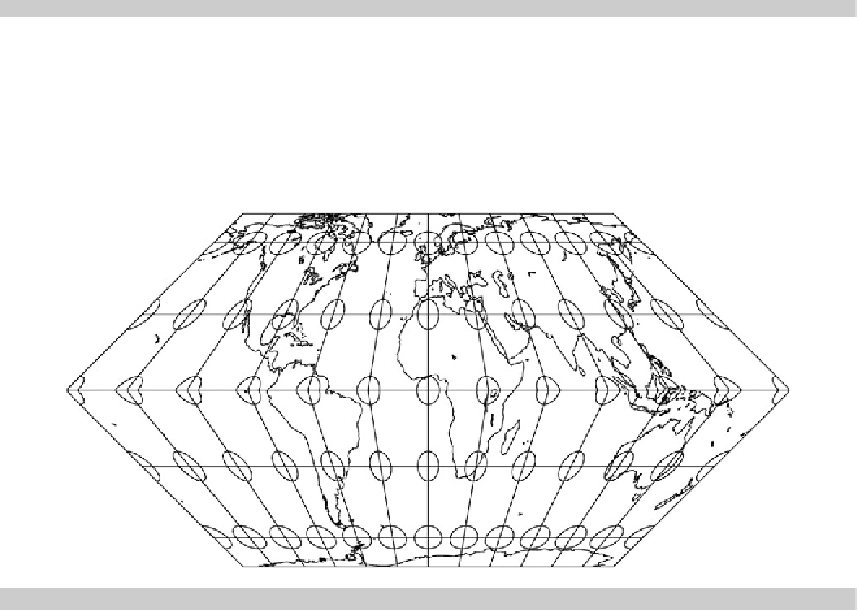
Fig. 1.9. Special pseudo-cylindrical projection of the sphere of type Eckert II ( Eckert 1906 ), Tissot ellipses of
distortion

Solution (the first problem).

Let us rewri te t he mapping eq uation s in a more systematic form by introducing the two constants

c 1 := 2 R/ √ 6 π and c 2 := R 2 π/ 3inBox 1.9 in order to analyze the graticule of “Eckert II”.
Fi rst, the geo metrical shape of the image of the meridians is determined by removing the root

4

from the second equation by substituting the root from the first equation. For
Λ = constant, we are led to the straight line L 1 ( Λ = constant). Second, the parallel circles
are immediately fixed in shape by Φ = constant. x is a homogeneous linear form of longitude
Λ and y is a constant. In summary, the meridians are tilted straights and the parallel circles
are parallel straights. Third, let u s c ompute the length of the circular equator x ( Λ =+ π,Φ =

− 3sin | Φ |

0) − x ( Λ = −π,Φ =0)=8 Rπ/ √ 6 π =4 πc 1 , the length of the central meridian x ( Λ =0 ,Φ =