Geography Reference
In-Depth Information
E
2
A
1
,A
2
, semi-major axis
A
1
, semi-minor
axis
A
2
; meridian of reference
L
01
and
L
02
, respectively, reference points
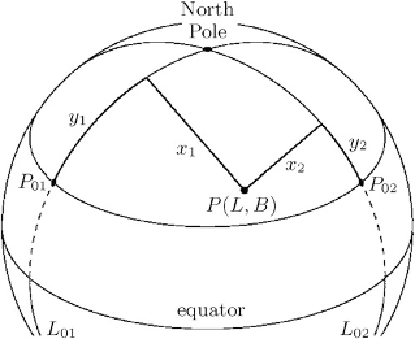
Fig. 15.18.
Oblique orthogonal projection of an ellipsoid-of-revolution
{
L
01
,B
01
=
B
0
}
and
{
L
02
,B
02
=
B
0
}
,
E
2
A
1
,A
2
respectively;
L
01
-strip,
L
02
-strip; a point
P
(
L,B
)on
15-611 The First Step: Polynomial Representation of Conformal Coordinates in the First Strip
and Bivariate Series Inversion
The standard polynomial representation of conformal coordinates of type Gauss-Krueger or UTM
in the
L
01
-strip is given by (
15.109
)and(
15.110
) subject to the longitude/latitude differences
l
1
;=
L
B
01
with respect to the longitude
L
01
of the reference meridian and
the latitude
B
01
of the reference point
−
L
01
and
b
1
;=
B
−
{
L
01
,B
01
}
of series expansion.
Easting :
(15.109)
x
1
=
ρ
(
x
10
l
1
+
x
11
l
1
b
1
+
x
30
l
1
+
x
12
l
1
b
1
+O
4
x
)
.
Northing :
(15.110)
y
1
=
ρ
(
y
0
+
y
01
b
1
+
y
20
l
1
+
y
02
b
1
+
y
03
b
1
+O
4
y
)
.
y
0
denotes the length of the meridian arc from zero ellipsoidal latitude to the ellipsoidal latitude
B
01
of the reference point
. The dilatation factor
ρ
amounts to one for a classical Gauss-
Krueger conformal mapping. Optimal alternative values for the dilatation factor depending on
the width of the strip, namely for UTM, are given in Box
15.9
. The coecients
{
L
01
,B
01
}
of the
conformal polynomial of type (
15.109
)and(
15.110
) of order five are derived in
Grafarend
(
1995
,
pp. 457-459), for instance, and listed in Boxes
15.4
and
15.5
. The length
y
0
of the meridian arc
from the equator to the reference point is computed from (
15.114
)inBox
15.10
.
{
x
ij
,y
ij
}

Search WWH ::

Custom Search