“Ellipsoid-of-Revolution to Cylinder”: Transverse Aspect - Map Projections: Cartographic Information Systems - page 351

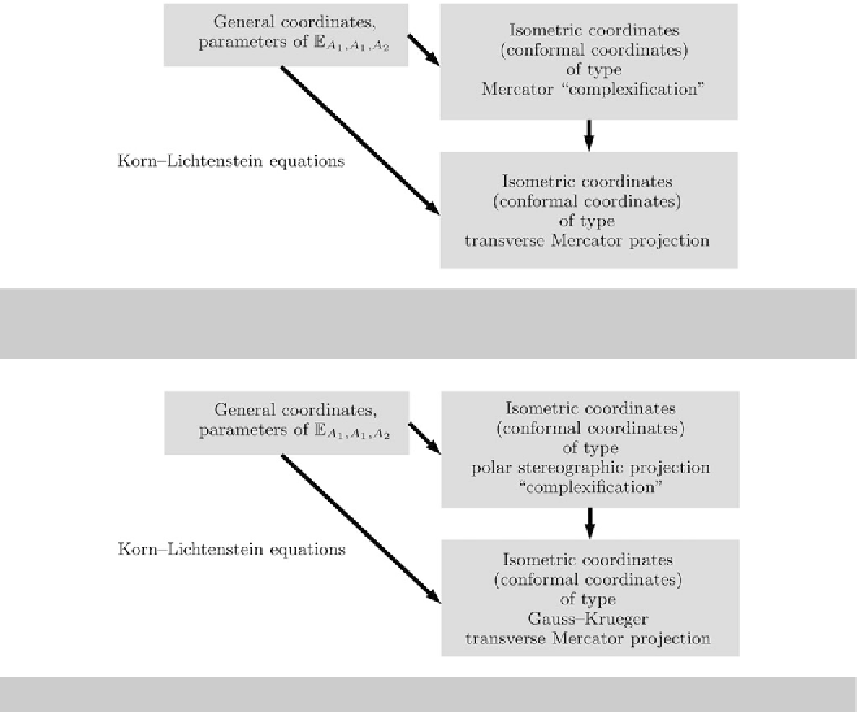
Fig. 15.1. Change from one conformal chart to another conformal chart (c:c: Cha-Cha-Cha) according to a
proposal by Gauss ( 1822 , 1844 ). First conformal coordinates: Mercator projection. Second conformal coordinates:
transverse Mercator projection. Ellipsoid-of-revolution E A 1 ,A 1 ,A 2

Fig. 15.2. Change from one conformal chart to another conformal chart (c:c: Cha-Cha-Cha) according to a
proposal by Krueger ( 1922 ). First conformal coordinates: polar stereographic projection. Second conformal coor-
dinates: transverse Mercator projection. Ellipsoid-of-revolution E A 1 ,A 1 ,A 2

In Grafarend ( 1995 ), we give two counterexamples of surfaces of revolution which are from the
differentiability class C ∞ , but which are not analytical. Accordingly, the theory of holomorphic

functions does not apply. Finally, one encounters great diculties in generalizing the theory of con-
formal mappings to higher-dimensional (pseudo-) Riemann manifolds. Only for even-dimensional
(pseudo-)Riemann manifolds of analytic type, multidimensional complex analysis can be estab-
lished. We experience a total failure for odd-dimensional (pseudo-)Riemann manifolds as they
appear in the theory of refraction, Newton mechanics, or plumb line computation, to list just
a few conformally flat three-dimensional Riemann manifolds. The theory of conformal mapping
took quite a different direction when Korn ( 1914 )and Lichtenstein ( 1911 , 1916 ) set up their
general differential equations for two-dimensional Riemann manifolds, which govern conformality.
They allow the straightforward transformation of ellipsoidal coordinates of type surface normal
longitude L and latitude B into conformal coordinates of type Gauss-Krueger or UTM ( x, y )
without any intermediate conformal coordinate system of type UMP or UPS! Accordingly, our
objective here is a proof of our statement!