Geography Reference
In-Depth Information
8-2 Special Mapping Equations
Setting up special mappings “ellipsoid-of-revolution to plane”, equidistant mapping, confor-
mal mapping, equiareal mapping.
8-21 Equidistant Mapping
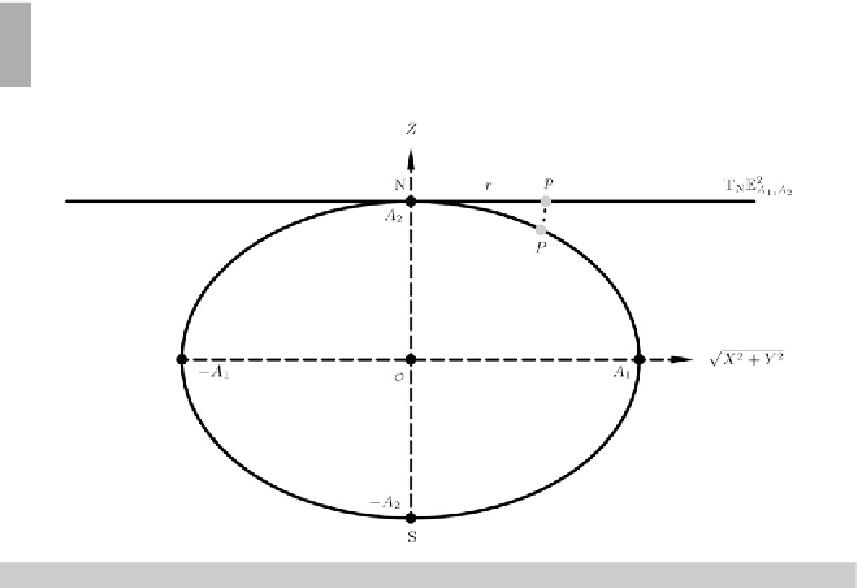
Let us postulate an
equidistant mapping
of the family of elliptic meridians
Λ
= constant, namely
r
=
f
(
Δ
), by means of the canonical postulate of an equidistant mapping
Λ
2
= 1. Figure
8.1
is
an illustration of such a mapping, and Box
8.3
contains the mathematical details of the mapping
equations
x
=
f
(
Δ
)cos
Λ
and
y
=
f
(
Δ
)sin
Λ
, where the radial function is given as an elliptic
integral of the second kind
f
(
Δ
∗
)=
A
1
E
(
Δ
∗
,E
)
,
(8.19)
where
Δ
∗
is the
circle reduced polar distance
and
E
is the
elliptic modulus
. Here, we address the
reader to Appendix C, where some notes on elliptic functions and elliptic integrals of the first,
second, and third kind are presented. At this point, we are left with the question of focal interest.
Question: “How can we prove the meridian arc length as an
elliptic integral of the second kind?” Answer: “Let us work
out this in the following passage in more detail.”
Fig. 8.1.
Equidistant mapping of the ellipsoid-of-revolution to the tangential plane: normal aspect, meridian
arc length
r
=
f
(
Δ
)
,P∈
E
2
A
1
,A
2

Search WWH ::

Custom Search