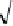Information Technology Reference
In-Depth Information
binary window method the string of
k
≥ 2 binary units (0, 1, 1, …, 1, 1) is replaced
with the string of
k
+ 1 signed binary digits (1, 0, 0, …, 0, -1). The higher radix ex-
ponent method uses radix of the form 2
d
, where
d
is relatively small, for example,
d
= 4. Firstly points 2
Q
, 3
Q
, …, (2
d
-1)
Q
are computed. Secondly exponent number is
represented in 2
d
-base notation, so only
(log
2
point additions are needed.
For affine point doubling and addition inversion in
F
q
is needed. This operation is
relatively slow. Projective coordinates exclude inversion during doubling and addi-
tion; so inversion is needed only once, after all doublings and additions are done.
Doubling (and addition) requires addition, subtraction and multiplication in
F
q
. The
first two operations are of linear complexity and the third one is of quadratic com-
plexity, so the rate of elliptic curve arithmetic depends on the number of multiplica-
tions. Doubling and addition need 12 and 15 field multiplications respectively [8].
Elliptic curves with
j
= 0 and
j
= 1728 possess complex multiplication. So to com-
pute
kQ
we represent exponent
k
as
k
≡
k
0
+
w
k
1
(mod
r
), where
w
is an eigenvalue of
complex multiplication operator, and
r
)
d
k
<
r
,
k
<
r
. We can use common base
0
1
(
2
2 for
k
0
and
k
1
. Point multiplication, performed as
k
0
Q
,
k
1
Q
,
wk
1
Q
,
k
0
Q
+
wk
1
Q
[8], is faster than commonly used multiplication.
We introduce a large class of elliptic curves with fast complex multiplication in-
stead of doubling and a simple algorithm, establishing bijection between the field
F
r
and the subset of polynomials of degree ≤
r
- 1 over {-1, 0, 1}.
log
r
)
2
Q
of points
Q
, 2
Q
, …,
3
1728
⋅
4
A
Elliptic curve
E
(
F
p
):
y
2
=
x
3
+
Ax
2
+
Bx
is defined by
j
-invariant
j
=
3
2
4
A
+
27
B
up to isomorphism. This curve over
F
has isogeny of degree 2: rational map
, under which
P
∞
→
P
∞
(in practice it is sufficient to consider curve
over
F
p
or its quadratic extension). Isogeny kernel is a set of
E
(
F
)
→
E
(
F
)
p
1
p
E
F
(
)
-points, mapping
p
to
P
∞
; it consists of four points of order 2.
For isogeny
E
E
1
curves
E
,
E
1
are called isogenious. The set of curves, isogen-
ious to the given curve
E
with invariant
j
, is given by
F
p
-roots of modular polynomial
→
Φ
2
(
u
,
v
) =
u
3
+
v
3
-
u
2
v
2
+ 1488
uv
(
u
+
v
) - 162000(
u
2
+
v
2
) + 40773375
uv
+
+ 8748000000(
u
+
v
) - 157464000000000 ,
if we set
v
=
j
. These roots are
j
-invariants of elliptic curves, which have isogeny of
degree 2 with
E
. If
j
is a root of
Φ
2
(
u
,
j
), then isogeny maps elliptic curve into itself
and corresponds to complex multiplication by non-real quadratic integer with the
norm 2. There exist two quadratic integers of this kind:
−
2
and
(
+
−
7
)
2
.
Let
E
(
F
p
) be elliptic curve over prime finite field with one parameter
t
:
y
2
=
x
3
- 4
tx
2
+ 2
t
2
x
.
(1)
It is known [9] that if