Geoscience Reference
In-Depth Information
Figure 2.3.
Example of (a) probability density function, and (b) cumulative
distribution function.
2.3.2
Fuzzy set theory
In classical, or crisp, set theory any element
x
of the universal set
X
can be classified as
being either an element of some sub-set
A
(
x A
) or an element of its complement (
x
i.e.
x
A
). In other words, the transition for an element in the universe between
membership and non-membership in a given set is abrupt and well-defined (hence called
crisp
) with membership either 1 (which certainly belongs to the set) or 0 (which certainly
does not belong to the set). In many practical situations it is more logical to define the
boundaries of sets vaguely so that an element can still be a member of a set with a degree
of membership other than 1. This concept was first implemented by Zadeh (1965) with
the introduction of
fuzzy set theory
. In fuzzy sets, therefore, the transition between the
membership and non-membership can be gradual. This gradual transition of memberships
is due to the fact that the boundaries of fuzzy sets are defined imprecisely and vaguely.
This property of a fuzzy set makes the fuzzy set theory viable for the representation of
uncertainty in a nonprobabilistic form.
Membership function
The essence of a fuzzy set, therefore, is the
membership
associated with the elements of
the set. Membership is defined as the
degree of belief,
also called
belief level,
to which
the element belongs to the set. The degree of belief or belief level or membership may take
any value between and including 0 and 1:0 meaning no membership and 1 meaning full
membership.
In order to define a fuzzy set formally, let
X
be a universe set of
x
values
(elements). Then
Ã
is called a fuzzy (sub)set of
X,
if
Ã
is a set of ordered pairs:
(2.12)
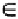

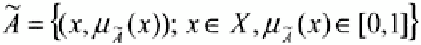


Search WWH ::

Custom Search