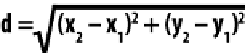Math, Physics, and Animation - HTML5 Canvas - page 174

Moving Between Two Points: The Distance of a Line
Movement based on constant changes to the x or y position of an object works well for
some applications, but other times you will need to be more precise. One such instance
is when you need to move an object from point A to point B at a constant rate of speed.
In mathematics, a common way to find the length of an unknown line is to use the
Pythagorean theorem:
A 2 + B 2 = C 2
In this equation, C is the unknown side of a triangle when A and B are already known.
However, we need to translate this equation into something we can use with the points
and pixels we have available on the canvas.
This is a good example of using a mathematical equation in your application. In this
case, we want to find the distance of a line, given two points. In English, this equation
reads like this:
The distance equals the square root of the square of the difference between the x value
of the second point minus the x value of the first point, plus the square of the difference
between the y value of the second point minus the y value of the first point.
You can see this in Equation 5-1 . It's much easier to understand in this format.
Equation 5-1. Distance equation
In the second example, we need to create some new variables in the canvasApp() func-
tion. We will still use a speed variable, just like in the first example, but this time we
set it to 5 , which means it will move 5 pixels on every call to drawScreen() :
var speed = 5;
We then create a couple dynamic objects—each with an x and a y property—that will
represent the two points we want to move between. For this example, we will move
our circle from 20 , 250 to 480 , 250 :
var p1 = {x:20,y:250};
var p2 = {x:480,y:250};
Now it is time to re-create the distance equation in Equation 5-1 . The first step is to
calculate the differences between the second and first x and y points:
var dx = p2.x - p1.x;
var dy = p2.y - p1.y;