Image Processing Reference
In-Depth Information
N
-1
2
2
-
j
xu
1
N
Fp
u
=
Ae
(2.16)
N
x
=0
And since the sum of a geometric progression can be evaluated according to:
a
(1 -
r
r
n
+1
)
n
k
k
0
ar
=
(2.17)
0
1 -
=0
the discrete Fourier transform of a sampled pulse is given by:
2
N
-
j
u
N
2
A
N
1 -
e
Fp
u
=
(2.18)
2
-
j
u
N
1 -
e
By rearrangement, we obtain:
u
1 -
2
sin(
u
uN
/ 2)
A
N
-
j
2
N
Fp
u
=
e
(2.19)
sin(
/
)
The modulus of the transform is:
sin(
u
uN
/ 2)
A
N
|
Fp
u
| =
)
(2.20)
sin(
/
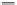
since the magnitude of the exponential function is 1. The original pulse is plotted in Figure
2.11
(a) and the magnitude of the Fourier transform plotted against frequency is given in
Figure
2.11
(b).
1 fx < 5
0
Fp
u
otherwise
x
(a) Sampled pulse
u
(b) DFT of sampled pulse
Figure 2.11
Transform pair for sampled pulse
This is clearly comparable with the result of the continuous Fourier transform of a pulse,
Figure
2.3
, since the transform involves a similar, sinusoidal, signal. The spectrum is
equivalent to a set of sampled frequencies; we can build up the sampled pulse by adding
up the frequencies according to the Fourier description. Consider a signal such as that
shown in Figure
2.12
(a). This has no explicit analytic definition, as such it does not have
a closed Fourier transform; the Fourier transform is generated by direct application of
Equation 2.15. The result is a set of samples of frequency, Figure
2.12
(b).