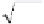Image Processing Reference
In-Depth Information
Since the errors are
independent
, the
compound
distribution of these errors is the product
of their distributions, and is given by
˜
2
˜
2
˜
2
˜
2
- ((
f
)
+(
f
)
+(
f
)
+...+(
f
N
)
)
1
2
3
1
2
˜
2
pf
() =
e
(9.17)
Each of the errors is a function of the unknown quantity,
a
, which is to be estimated.
Different estimates of
a
will give different values for
p
(
˜
. The most probable system of
errors will be that for which
p
(
˜
is a
maximum
, and this corresponds to the
best
estimate
of the unknown quantity. Thus to maximise
p
()
˜
˜
˜
˜
˜
2
2
2
2
- ((
f
)
+(
f
)
+(
f
)
+...+(
f
N
) )
1
2
3
1
2
˜
2
max{
pf
(
)} = max
e
˜
˜
˜
˜
2
2
2
2
- ((
f
)
+(
f
)
+(
f
)
+...+(
f
N
) )
1
2
3
2
= max
e
(9.18)
˜
˜
˜
˜
2
2
2
2
= max{-((
f
)
+ (
f
)
+ (
f
)
+ . . . + (
f
N
) )}
1
2
3
˜
˜
˜
˜
f f f f
N
Thus the required estimate is that which
minimises
the sum of the differences squared and
this estimate is the one that is
optimal
by the least squares criterion.
This criterion leads on to the method of least squares which follows in the next section.
This is a method commonly used to fit curves to measured data. This concerns estimating
the values of parameters from a complete set of measurements. There are also techniques
which provide estimate of parameters at time instants, based on a set of previous measurements.
These techniques include the Weiner filter and the Kalman filter. The Kalman filter was the
algorithm chosen for guiding Exocet missiles and moon missions (an extended square root
Kalman filter, no less).
= min{(
)
2
+ (
)
2
+ (
)
2
+ . . . + (
) }
2
1
2
3
9.2.2
Curve fitting by least squares
Curve fitting
by the method of least squares concerns combining a set of measurements to
derive
estimates
of the parameters which specify the curve which best fits the data. By the
least squares criterion, given a set of
N
(noisy) measurements
f
i
i
1,
N
which are to be
fitted to a curve
f
(
a
) where
a
is a vector of parameter values, we seek to minimise the
square of the difference between the measurements and the values of the curve to give an
estimate of the parameters
a
according to
N
Σ
i
a
2
= min
(
f
- (
f
xy
,
,
a
))
(9.19)
i
i
i
=1
Since we seek a minimum, by differentiation we obtain
N
(
f
- (
f
xy
a
, , ))
2
i
i
i
i
=1
= 0
(9.20)
a