Neighborhood Processing - Introduction to Video and Image Processing - page 86

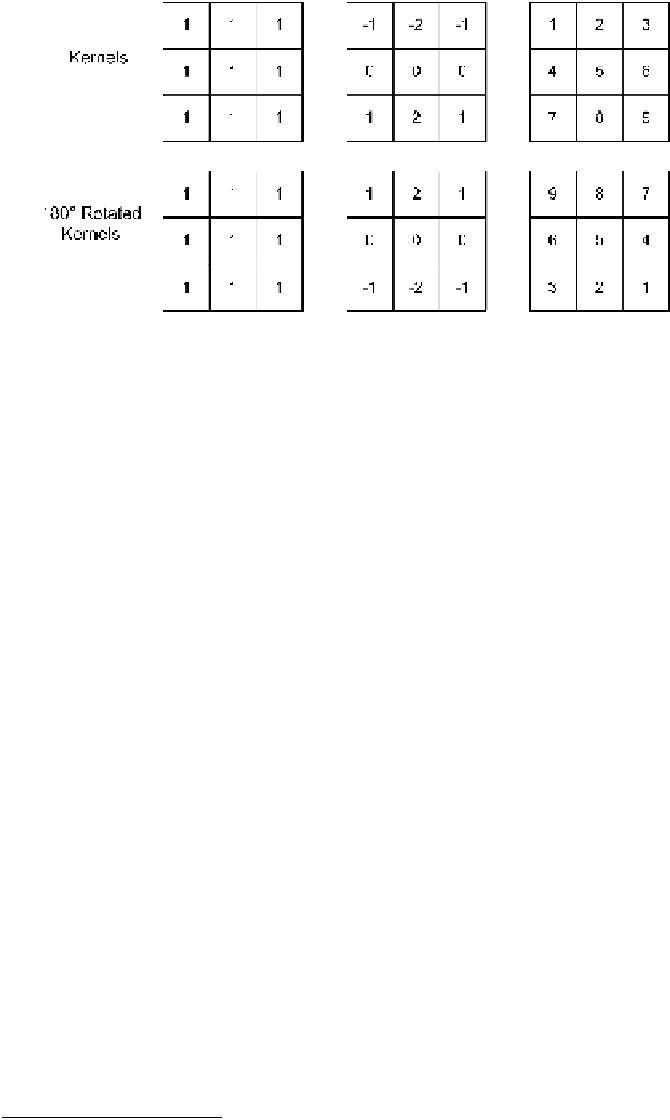
Fig. 5.19 Three kernels and their rotated counterparts
Comparing this to the equation for correlation in Eq. 5.4 we can see that the
only differences are the two minus signs. The interpretation of these is that the
kernel is rotated 180° before doing a correlation. In Fig. 5.19 examples of rotated
kernels are shown. What we can see is that symmetric kernels are equal before and
after rotation, and hence convolution and correlation produce the same result. Edge
detection kernels are not symmetric. However, since we often only are interested in
the absolute value of an edge the correlation and convolution again yield the same
result.
When applying smoothing filters, finding edges etc. the process is often denoted
convolution even though it is often implemented as correlation! When doing tem-
plate matching it is virtually always denoted correlation.
One might rightfully ask why convolution is used in the first place. The answer
is that from a general signal processing 5 point of view we actually do convolution,
and correlation is convolution done with a rotated kernel. However, since correlation
is easier to explain and since it is most often what is done in practice, it has been
presented as though it were the other way around in this (and many other) texts. The
technical reasons for the definition of convolution are beyond the scope of this text
and the interested reader is referred to a general signal processing textbook.
Edge detection is a key method in many image processing systems and a number
of different methods have therefore been suggested over the years. Using the Sobel
kernels works well, but results in wide edges as can bee seen in Fig. 5.17 .Ifwe
are interested in knowing the exact edge, i.e., a 1-pixel thin edge, then the same
figure suggests to use the second order derivatives and look for the places where the
values change from positive to negative or vise versa. These places are denoted zero-
crossings . As mentioned above the first order derivatives are sensitive to noise in the
images. This problem is even more profound for the second order derivatives. The
5 Image processing is a subset of signal processing.