Image Processing Reference
In-Depth Information
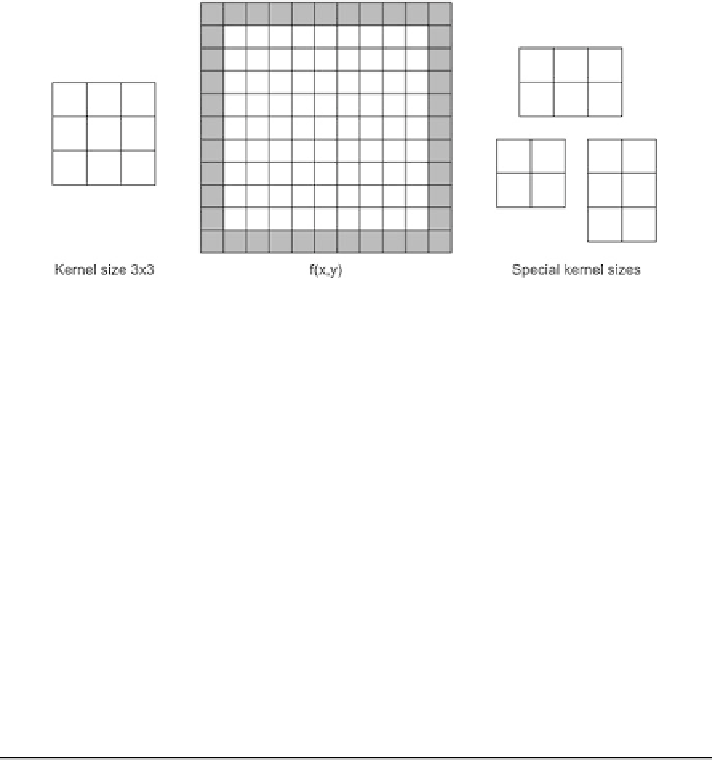
Fig. 5.5
An illustration of the border problem, which occurs when using neighborhood processing
algorithms. If a kernel with a size of 3
3 is used, then the border illustrated in
f(x,y)
cannot be
processed. One solution to this is to apply kernels with special sizes on the borders, like the ones
showed to the
right
×
5.1.1 Rank Filters
The Median Filter belongs to a group of filters known as
Rank Filters
. The only
difference between them is the value which is picked after the pixels have been
sorted:
The minimum value
This filter will make the image darker.
The maximum value
This filter will make the image brighter.
The difference
This filter outputs the difference between the maximum and min-
imum value and the result is an image where the transitions between light and
dark (and opposite) are enhanced. Such a transition is often denoted an edge in an
image. More on this in Sect.
5.2.2
.
5.2
Correlation
Correlation
is an operation which also works by scanning through the image and
applying a filter to each pixel. In correlation, however, the filter is denoted a
kernel
and plays a more active role. First of all the kernel is filled by numbers—denoted
kernel coefficients
. These coefficients weight the pixel value they are covering and
the output of the correlation is a sum of weighted pixel values. In Fig.
5.6
some
different kernels are shown.
Similar to the median filter the kernel is centered above the pixel position whose
value we are calculating. We denote this center
(
0
,
0
)
in the kernel coordinate system
and the kernel as
h(x,y)
, see Fig.
5.7
. To calculate the output value we take the
value of
h(
1
)
and multiply it by the pixel value beneath. Let us say that we
are calculating the output value of the pixel at position
(
2
,
2
)
. Then
h(
−
1
,
−
1
)
will
be above the pixel
f(
1
,
1
)
and the value of these two pixels are multiplied together.
The result is added to the product of the next kernel element
h(
0
,
−
1
,
−
−
1
)
and the pixel