Neighborhood Processing - Introduction to Video and Image Processing - page 72

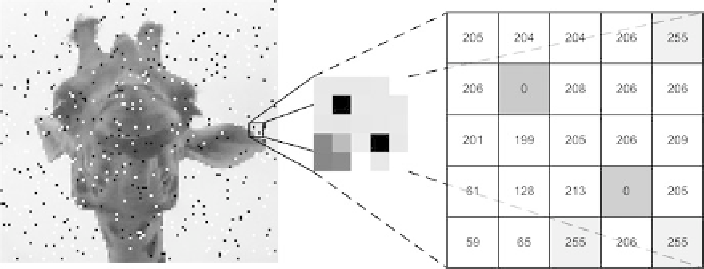
Fig. 5.3 An image infected with salt-and-pepper noise. The noise is easily recognized in both the
image- and the number representations

The next question is how to find the noise pixels in order to know where to per-
form the median operation. For the particular example we could scan the image
pixel-by-pixel and look for isolated values of 0 or 255. When encountered, the me-
dian operation could be applied. In general, however, a pixel with a value of say
234 could also be considered noise if it is isolated (stands out from its neighbors).
Therefore, the median operation is applied to every single pixel in the image and we
call this filtering the image using a median filter . Filtering the image refers to the
process of applying a filter (here the median filter) to the entire image. It is important
to note that by filtering the image we apply the filter to each and every pixel.
When filtering the image we of course need to decide which operation to apply
but we also need to specify the size of the filter. The filter used in Fig. 5.2 is a
3 3 filter. Since filters are centered on a particular pixel (the center of the filter)

the size of the filter is uneven, i.e., 3, 5, 7, etc. Very often filters have equal spatial
dimensions, i.e., 3

×

7, etc. Sometimes a filter is described by its radius
rather than its size. The radius of a 3

× 3, 5 × 5, 7 ×

7
filter etc. The radius/size of a filter controls the number of neighbors included. The
more neighbors included, the more strongly the image is filtered. Whether this is
desirable or not depends on the application. Note that the larger the size, the more
processing power is required by the computer. Applying a filter to an image is done
by scanning through the image pixel-by-pixel from the upper left corner toward the
lower right corner, as described in the previous chapter. Figure 5.4 shows how the
image in Fig. 5.3 is being filtered by a 3

× 3filteris1,2fora5 × 5filter,3fora7 ×

× =

3 ( radius 1 ) mean and median filter,

respectively. Note the superiority of the median filter.
In terms of programming, the Median filter can be implemented as illustrated
below—here exemplified in C-code:

for (y = Radius ; y < (M − Radius ); y = y + 1)

{

−

for (x = Radius ; x < (N Radius ); x = x + 1)

{