Image Processing Reference
In-Depth Information
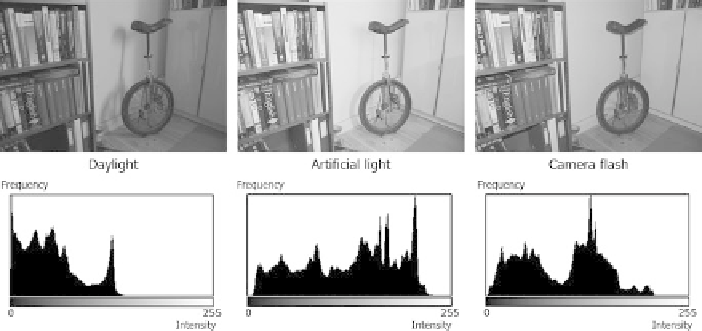
Fig. 4.20
Three images of the same scene with different illuminations and hence different his-
tograms
Chap. 2. Imagine a white object is entering a scene where the background is dark.
As more and more of the object becomes visible in the scene the auto gain func-
tion will decrease the brightness accordingly in order to keep the overall brightness
constant. This means that the threshold value needs to be changed from image to
image and often rather significantly. Such significant changes can sometimes be
handled by preforming a histogram stretching/equalization. This only works when
the changes result in a shifted histogram (making the image brighter or darker) with-
out changing the structure of the histogram. An example of a changed structure is
when light from multiple windows illuminate the objects in the scene differently
over time. In Fig.
4.20
examples of different illuminations of the same scene are
shown.
Automatic Thresholding: Global Method
As mentioned above, thresholding is based on the notion that an image consists of
two groups of pixels; those from the object of interest (foreground) and those from
the background. In the histogram these two groups of pixels result in two “moun-
tains” denoted modes. We want to select a threshold value somewhere between these
two modes. Automatic methods for doing so exist and they are based on analyzing
the histogram, i.e. all pixels are involved, and hence denoted a
global
method. The
idea is to try all possible threshold values and for each, evaluate if we have two good
modes. The threshold value producing the best modes is selected. Different defini-
tions of “good modes” exits and here we describe the one suggested by Otsu [14].
The method evaluates Eq.
4.15
for each possible threshold value
T
and select the
T
where
C(T )
is minimum. The reasoning behind the equation is that the correct
threshold value will produce two narrow modes, whereas an incorrect threshold
value will produce (at least one) wide mode. The narrowness of a mode can be
measured by the variance
σ
2
, see Appendix C for a definition of
σ
2
. So the smaller
the variances the better. To balance the measure, each variance is weighted by the