Image Processing Reference
In-Depth Information
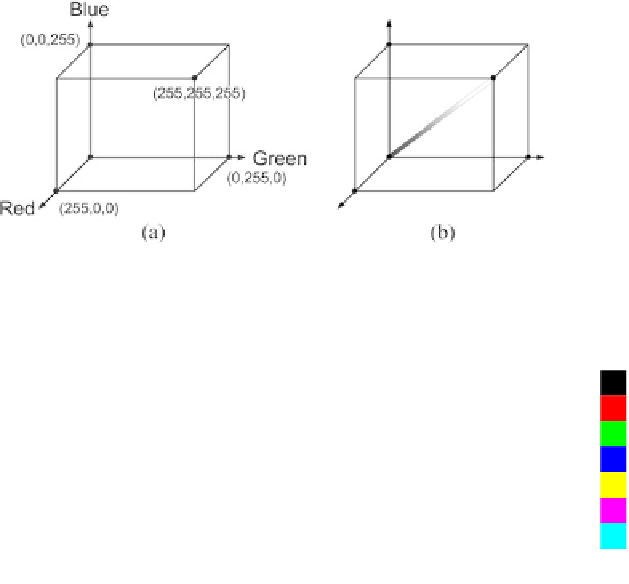
Fig. 3.7
(
a
) The RGB color cube. (
b
) The gray-vector in the RGB color cube
Table 3.2
The colors of the
different corners in the RGB
color cube
Corner
Color
(
0
,
0
,
0
)
Black
(
255
,
0
,
0
)
Red
(
0
,
255
,
0
)
Green
(
0
,
0
,
255
)
Blue
(
255
,
255
,
0
)
Yellow
(
255
,
0
,
255
)
Magenta
(
0
,
255
,
255
)
Cyan
(
255
,
255
,
255
)
White
3.2.1 The RGB Color Space
According to Eq.
3.1
a color pixel has three values and can therefore be represented
as one point in a 3D space spanned by the three colors. If we say that each color
is represented by 8-bits, then we can construct the so-called RGB color cube, see
Fig.
3.7
.
In the color cube a color pixel is one point or rather a vector from
(
0
,
0
,
0
)
to
the pixel value. The different corners in the color cube represent some of the
pure
colors
and are listed in Table
3.2
. The vector from
(
0
,
0
,
0
)
to
(
255
,
255
,
255
)
passes
through all the gray-scale values and is denoted the
gray-vector
. Note that the gray-
vector is identical to Fig.
3.2
.
3.2.2 Converting from RGB to Gray-Scale
Even though you use a color camera it might be sufficient for your algorithm to ap-
ply the intensity information in the image and you therefore need to convert the color
image into a gray-scale image. Converting from RGB to gray-scale is performed as
I
=
W
R
·
R
+
W
G
·
G
+
W
B
·
B
(3.3)