Image Acquisition - Introduction to Video and Image Processing - page 11

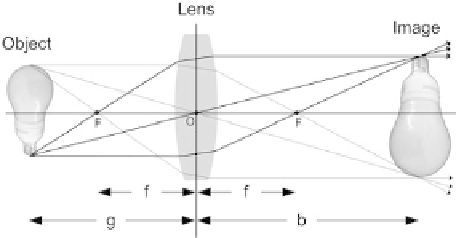
Fig. 2.6 The figure shows
how the rays from an object,
here a light bulb, are focused
via the lens. The real light
bulb is to the left and the
image formed by the lens is to
the right

at a distance very close to the focal point. Equation 2.2 is also called the thin lens
equation .
Another interesting aspect of the lens is that the size of the object in the image,
B , increases as f increased. This is known as optical zoom . In practice f is changed
by rearranging the optics, e.g., the distance between one or more lenses inside the
optical system. 1 In Fig. 2.7 we show how optical zoom is achieved by changing the
focal length. When looking at Fig. 2.7 it can be shown via similar triangles that

b
B =

g
G

(2.3)

where G is the real height of the object. This can for example be used to compute
how much a physical object will fill on the imaging censor chip, when the camera is
placed at a given distance away from the object.
Let us assume that we do not have a zoom-lens, i.e., f is constant. When we
change the distance from the object to the camera (lens), g ,Eq. 2.2 showsusthat b
should also be increased, meaning that the sensor has to be moved slightly further
away from the lens since the image will be formed there. In Fig. 2.8 the effect of not
changing b is shown. Such an image is said to be out of focus . So when you adjust
focus on your camera you are in fact changing b until the sensor is located at the
position where the image is formed.
The reason for an unfocused image is illustrated in Fig. 2.9 . The sensor consists
of pixels, as will be described in the next section, and each pixel has a certain size.
As long as the rays from one point stay inside one particular pixel, this pixel will be
focused. If rays from other points also intersect the pixel in question, then the pixel
will receive light from more points and the resulting pixel value will be a mixture of
light from different points, i.e., it is unfocused.
Referring to Fig. 2.9 an object can be moved a distance of g l further away from
the lens or a distance of g r closer to the lens and remain in focus. The sum of g l and
g r defines the total range an object can be moved while remaining in focus. This
range is denoted as the depth-of-field .

1 Optical zoom should not be confused with digital zoom, which is done through software.