Image Processing Reference
In-Depth Information
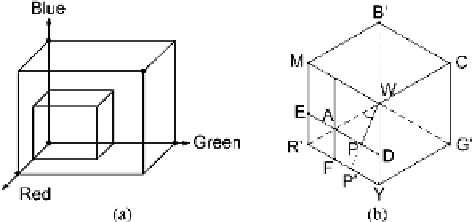
Fig. E.1
(
a
) The sub-cube inside the RGB color cube. (
b
) The hexagon defined when looking
at the sub-cube from the point
(
255
,
255
,
255
)
and toward the point
(
0
,
0
,
0
)
. The corners of the
hexagon correspond to the corners of the sub-cube. The
dashed lines
indicate the lines not visible
if the sub-cube is solid
Fig.
E.1
(b), meaning that we can derive hue and saturation in the two sextants from
Fig.
E.1
(b) and then directly express hue and saturation in terms of the RGB values.
Similar arguments can be made for the remaining sextants.
E.1.1 HSV: Saturation
Looking at Fig.
E.1
(b) saturation is defined as the ratio between the distance from
the
W
to
P
and the distance from
W
to
P
, where
P
is the intersection between the
vectors spanned by
W
and
P
, and
R
and
Y
. That is, saturation is given as
−−
WP
−−
WP
S
=
(E.2)
Since the triangles
WPD
and
WP
Y
are similar, see Appendix
B
,wehave
|
−−
WP
=
−−
WD
−−
WP
S
=
(E.3)
−−
WY
From this follows that
=
−−
WD
=
−−
WY
−
−
DY
S
(E.4)
−−
WY
−−
WY
−−
WY
We know from the definition of the sub-cube that
=
V
and can see in
−
DY
Fig.
E.1
(b) that
=
B
. This yields
S
=
(V
−
B)/V
. We can see that
B
=
min
{
R,G,B
}
in the sextant where
P
is located and can therefore express saturation
as