Image Processing Reference
In-Depth Information
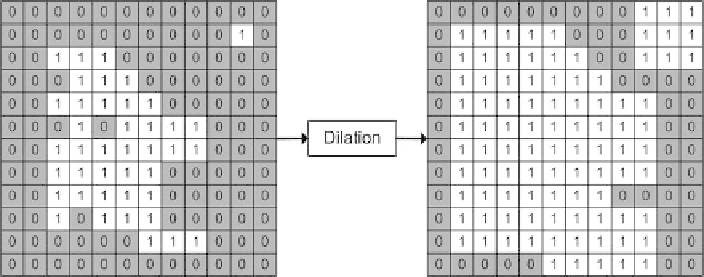
Fig. 6.5
Dilation of the binary image in Fig.
6.4
using
S
1
The term
dilation
refers to the fact that the object in the binary image is increased
in size. In general, dilating an image results in objects becoming bigger, small holes
being filled, and objects being merged. How big the effect is depends on the size
of the structuring element. It should be noticed that a large structuring element can
be implemented by iteratively applying a smaller structuring element. This makes
sense since Eq.
6.2
holds. The equation states that dilating twice with
SE
1
is similar
to dilating one time with
SE
2
, where
SE
2
is the same type but has twice the radius
of
SE
1
. For example, if
SE
2
is a 5
×
5 structuring element, then
SE
1
is a 3
×
3, etc.
SE
2
≈
f(x,y)
SE
1
⊕
f(x,y)
⊕
⊕
SE
1
(6.2)
In Fig.
6.5
the binary image in Fig.
6.4
is dilated using the structuring element
S
1
. First of all we can see that the object gets bigger. Secondly we can observe that
the hole and the convex parts of the object are filled, which makes the object more
compact.
In Fig.
6.6
a real image is dilated with different sized box-shaped structuring
elements. Again we can see that the object is becoming bigger and that holes inside
the person are filled. What is, however, also apparent is that the noisy small objects
are also enlarged. Below we will return to this problem.
6.2.2 Erosion
Applying Fit to an entire image is denoted Erosion and is written as
g(x,y)
=
f(x,y)
SE
(6.3)
The term
erosion
refers to the fact that the object in the binary image is decreased
in size. In general, erosion of an image results in objects becoming smaller, small
objects disappearing, and larger objects splitting into smaller objects. As for dila-
tion the effect depends on the size of the structuring element and large structuring
elements can be implemented using an equation similar to Eq.
6.2
.