Information Technology Reference
In-Depth Information
Zu berechnen bleibt noch der Wert von d. Diese Größe tritt
jedoch auch als langer Schenkel
1
-
d
im großen Dreieck auf.
Durch nochmalige Anwendung des Satzes von Pythagoras
erhält man:
2
s
s
)
+
11
2
(
n
=−
d
Abb. 3.20
Approximative Berechnung von Pi
Durch Ausmultiplizieren und Umsortieren erhält man:
Die ersten Versuche, das Geheimnis des Verhältnisses zwi-
schen Durchmesser (bzw. Radius) und Umfang eines Kreises
zu lösen, erfolgten wohl auf experimentellem Wege. Mittels
einer Schnur zog man um einen Stab als Mittelpunkt einen
Kreis. Auf die Kreislinie stellte man Pfosten oder Stäbe und
legte dann um diese Umrundung eine zweite Schnur. Die
Länge der beiden Schnüre beschrieb das Verhältnis vom Ra-
dius zum Umfang. Die gleiche Methode wurde auf vorhandene
runde Gegenstände wie Bäume usw. angewandt. Nachdem alle
Versuche, durch systematisches Vervielfachen des Radius bzw.
des Durchmessers den Umfang zu berechnen, fehlschlugen,
erkannte man irgendwann, dass die Division dieser beiden
Größen stets zu dem annähernd gleichen Ergebnis führt.
Eine der ersten näherungsweisen Berechnungen der Kreis-
zahl Pi, die mit dieser Methode durchgeführt wurde, indet
sich bereits im
Moskauer Papyrus
und auch im
Papyrus Rhind
fast 2000 Jahre vor unserer Zeitrechnung. Der berühmte Philo-
soph und Naturwissenschaftler
Archimedes
(287-212 v. Chr.)
erfand eine Methode, mit der approximativ beliebig genau
ein Kreisumfang und damit Pi berechnet werden konnte. Er
grenzte den Kreisumfang mit Vielecken (bis zum 96-Eck)
konnte er genau berechnen und der Mittelwert ergab angenä-
hert den Kreisumfang. Er kam zu dem Ergebnis, dass Pi klei-
ner als 3 + 10/70 und größer als 3 + 10/71 sein muss. Diese
Erkenntnis war so herausragend, dass die Kreiszahl Pi in der
Folge auch als „Archimedes-Konstante“ bezeichnet wurde.
Allerdings ergibt sich bei dieser Methode das Problem der
Berechnung des Umfangs bzw. der Fläche der Polygone. Be-
reits Archimedes kannte jedoch den Trick, mit dem man den
Umfang eines 2n-Ecks einfach berechnen kann, wenn man
den Umfang des n-Ecks kennt (
Abb. 3.21
). Hierzu muss man
nur den Satz des Pythagoras trickreich anwenden. Ausgangs-
punkt der Berechnung ist ein Kreis mit dem Radius 1. Sein
Umfang ist damit 2 × Pi. Die Seitenlänge und der Umfang
eines n-Ecks, welches in den Kreis gelegt wird, seien be-
kannt. Halbiert man jeden der n Innenwinkel, so erhält man
ein 2n-Eck.
Die gesuchte Größe ist
s
2n
. Da dies die lange Seite in einem
rechtwinkligen Dreieck ist, gilt der Satz des Pythagoras:
2
dd
s
n
2
−+=
2
0
4
Die Gleichung besitzt zwei Lösungen. Da jedoch
d
kleiner
als 1 ist, ist nur die Lösung mit dem Minuszeichen relevant,
d. h. man erhält für d:
2
s
n
d
=− −
11
4
Da in der Formel für
s
2n
der Wert von
d
2
vorkommt, wird
zunächst dieser Wert berechnet:
2
2
s
2
n
d
=−−
11
4
2
2
s
s
n
n
=− −−
221
44
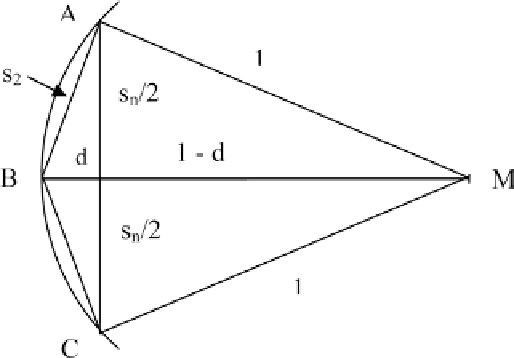
Abb. 3.21
Berechnung eines 2n-Ecks
2
=
s
+
2
2
n
s
d
2
n
2