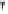Geoscience Reference
In-Depth Information
z
P
u
b
F
1
F
2
E
a
uE
2
+
2
el
Fig. 1.11. Reference ellipsoid and ellipsoidal-harmonic coordinates
If the eccentricity
E
reduces to zero, the ellipsoidal-harmonic coordinates
u, ϑ, λ
become spherical coordinates
r, ϑ, λ
; the ellipsoid
u
=
b
becomes the
sphere
r
=
R
because then the semiaxes
a
and
b
are equal to the radius
R
;
and we find
P
nm
i
u
E
Q
nm
i
u
E
=
R
r
n
+1
=
u
b
n
=
r
R
n
,
i
i
lim
E→
0
lim
E→
0
,
b
E
b
E
P
nm
Q
nm
(1-175)
so that the first series in (1-174) becomes (1-116), and the second series in
(1-174) becomes (1-117). Thus, we see that the function
P
nm
(
iu/E
) corre-
sponds to
r
n
and
Q
nm
(
iu/E
) corresponds to
r
−
(
n
+1)
in spherical harmonics.
Hence, the first series in (1-174) is harmonic in the interior of the ellipsoid
u
=
b
, and the second series in (1-174) is harmonic in its exterior; this case
is relevant to geodesy. For
u
=
b
, the two series are equal:
V
i
(
b, ϑ, λ
)=
V
e
(
b, ϑ, λ
)
∞
n
(1-176)
=
[
a
nm
P
nm
(cos
ϑ
)cos
mλ
+
b
nm
P
nm
(cos
ϑ
)sin
mλ
]
.
n
=0
m
=0
Thus, the solution of Dirichlet's boundary-value problem for the ellipsoid
of revolution is easy. We expand the function
V
(
b, ϑ, λ
), given on the ellip-
soid
u
=
b
, into a series of surface spherical harmonics with the following
arguments:
ϑ
= complement of reduced latitude,
λ
= geocentric longitude.
Then the first series in (1-174) is the solution of the interior problem and
the second series in (1-174) is the solution of the exterior Dirichlet problem.