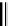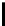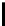Information Technology Reference
In-Depth Information
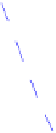
Ψ
(
n
)=
∂
∂n
ln
Γ
(
n
)
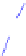
Vice versa, keeping the dimension fixed and differentiate term (2) with respect
to
r
, it is not solvable in roots, i.e. no extrema exists :
where
r
n
=
π
n/
2
Γ
2
+1
r
n
nπ
n/
2
rΓ
2
+1
∂
∂r
·
(4)
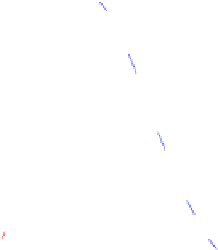
For instance a hypersphere with radius
r
= 1 reaches its maximum volume in
dimension 5 and looses volume in lower and higher dimensions. In figure 2 this
property is visualized for different radius lengths
r
=
.Onecan
see that for each radius length in dimension from
n
=0to
n
= 25, the associated
hypersphere reaches a maximal volume in a certain dimension and looses volume
asymptotically in higher and lower dimensions.
{
0
.
9
,
1
.
0
,
1
.
1
,
1
.
2
}
16
r = 1.2
12
r
=
1.1
8
r
=
1.0
4
r = 0.9
0
0
5
10
15
20
25
dimension
x
Fig. 2.
Hypersphere volume plot for radius lengths
r
=
{
0
.
9
,
1
.
0
,
1
.
1
,
1
.
2
}
and dimen-
sion
n
=0
,...,
25. Obviously,
n
is a nonnegative integer, but the graph is drawn
treating
n
as continuously varying.
Table 1.
Dimension where a hypersphere reaches the maximum volume for radius
lengths
r
=
{
0
.
05
,
0
.
1
,
0
.
2
,...,
1
.
0
}
. Results are obtained by considering term (3) as a
real-valued function.
Radius
r
0.05
0.1
0.2
0.3 0.4 0.5
0.6
0.7
0.8
0.9
1.0
-9.17
·
10
7
-88.94 1.59 1.12 1.0 1.03 1.20 1.53 2.14 3.23 5.27
Dimension
n
Table 1 presents the dimension where a hypersphere reaches its maximum
volume for different radius lengths. Surprisingly, for radius lengths
r
=0
.
05 and
r
=0
.
1 the maximum volume lies in negative real-valued numbers. Hence, a vol-
ume maximization for such small radius lengths is not feasible, as the dimension
is a nonnegative integer.