Graphics Reference
In-Depth Information
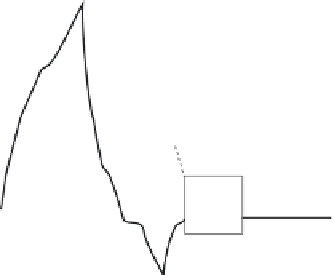
Figure 10.16
Wavelet basis function.
is the mother wavelet function (in one dimension), then other wavelet
functions are created as
If
ψ
(
x
)
x
;
1
√
a
ψ
−
b
ψ
a
,
b
(
x
)=
a
these are sometimes known as “child” or “daughter” wavelet functions. In 1D,
compact support means that the mother wavelet, and therefore all the child
wavelets, are nonzero only in a closed interval. Analogous to a wave, a weighted
sum of wavelets having different phase and scale (
a
and
b
, respectively) is used
to approximate a function. The functions in a wavelet basis are expected to be
orthogonal to facilitate projecting a function onto the basis functions. Because
of this, not every function works as a wavelet mother function, and the child
wavelets cannot be chosen arbitrarily. In fact, constructing mother wavelet func-
tions is a challenging task. The first orthogonal set of continuous wavelets having
compact support was constructed by mathematician Ingrid Daubechies in 1988.
Figure 10.16 illustrates a
Daubechies wavelet
. The child wavelets are scaled by
powers of two; i.e.
a
2
m
for integer
m
(higher-frequency wavelets correspond
=
to negative values of
m
).
The local nature of the basis functions are a key difference between wavelets
and spherical harmonics. In a region of the sphere having little detail, coefficients
of the high-frequency wavelets will be very small, or zero, and can therefore be
omitted. Conversely, many high-frequency wavelets may be needed to represent
high-frequency detail; however, they are only needed at the detailed areas and do
not affect the rest of the sphere. The compact support property thus allows detail
to be represented only where it is necessary. Detail of much higher frequency can
often be represented using the same number of coefficients required for a lower-