Information Technology Reference
In-Depth Information
c
c
a
a
b
b
(1)
(2)
(3)
a
b
a
b
(6)
(4)
(5)
(
)
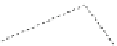
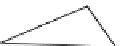
Fig. 7.
(1)
d
(
P
)ofaprism
P
whose base is an equilateral triangle and a triangle similar
to the base triangle
abc
; (2) a cut 2-complex with
abc
; (3) the unfolding of
d
(
P
)by
the cut 2-complex; (4) another cut 2-complex of
d
(
P
) with a line segment
ab
parallel
to side edges; (5) the unfolding of
d
(
P
) corresponding to (5); (6) a cut 2-complex of
d
(
P
)when
b
is on the face of
P
; (7) the unfolding of
d
(
P
) corresponding to the cut
2-complex shown in (6).
(1) a paral lelepiped,
(2) a triangular prism whose base is an equilateral triangle, a right triangle with
an a
n
gle
ˀ
/
3
, or a isosceles right triangle, or
(3) a
(
√
3
,
√
3
,
2)
-tetrahedron
ST
.
Any two convex unfoldings
W
and
X
of
d
(
P
)
are transformable to each other,
whereweassume
P
X
.If
W
divides
P
∗
into
n
(non-empty) pieces
by its corresponding cut 2-complex (where
n
is the number of edges of
P
),
W
is
reversible to
X
(Fig.
8
).
ↂ
W
and
P
ↂ
Proof.
Let
P
m
be the image of
P
by reflection in the plane ʠ including a face of
a reflective space-filler
P
. Then
P
P
m
is an unfolding of
d
(
P
) which includes
P
. Any unfolding
W
of
d
(
P
) satisfying
P
∪
P
m
by
ↂ
W
, is transformable to
P
∪
hinges
, which is proved by a similar process to the one shown in the pair of a
rhombic dodecahedron and a rectangular parallelepiped (see Fig.
3
). Notice that
the surface
∂W
is transformed to a subset
Y
in
P
m
and
Y
is mapped to the cut
2-complex for
W
in
P
∗
by reflection in ʠ.
Let
X
be a convex unfolding of
d
(
P
) with
P
m
H
X
(we assume
P
m
ↂ
ↂ
X
X
since
P
m
is strictly congruent to
P
). Dissect
P
in
W
by the
cut 2-complex which is strictly congruent to the cut 2-complex for
X
, and use
the hinges
instead of
P
ↂ
H
. Then
W
is transformed to
X
.




















































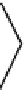











Search WWH ::

Custom Search