Information Technology Reference
In-Depth Information
Hence, we may assume that
|C|≤n −
1
for every
C ∈{R, B, G}.
Suppose that some two adjacent vertices
u
and
v
of
conv
(
X
) have distinct
colors. By our assumption, we have
|C ∩
(
X −{u, v}
)
|≤|C|≤n −
1
for every
C ∈{R, B, G}.
Thus, since
|X −{u, v}|
=2(
n −
1), we can apply the inductive hypothesis to
X −{u, v}
X −{u, v}
and there exists a Perfect Matching on
. By adding an edge
uv
to this matching, we can obtain the desired Perfect Matching.
Therefore, we may assume that all the vertices of
conv
(
X
) have the same
color. Let
v
be a vertex of
conv
(
X
). By a suitable rotation of the plane, we may
assume that
v
is the highest vertex of
conv
(
X
), and
a
and
b
are the left and the
right vertices of
conv
(
X
) adjacent to
v
, respectively.
We sort all the points of
X
with respect to their counterclockwise angle from
the ray emanating from
v
and passing through
a
, and denote the sorted sequence
by (
x
1
,x
2
,...,x
2
n
)sothat
x
1
=
v
,
x
2
=
a
,and
x
2
n
=
b
. Since the two end-points
x
1
and
x
2
n
have the same color, by Lemma
1.8
, there exists an even number
p
(2
≤ p ≤
2
n −
1) such that for every
C ∈{R, B, G}
,
2
|C ∩{x
1
,...,x
p
}| ≤
2
,
n − p
2
|C ∩{x
p
+1
,...,x
2
n
}| ≤
.
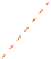
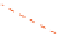
This implies that the line passing through
v
and
x
p
partitions
X \{v, x
p
}
into
Left
=
{x
2
(=
a
)
,x
3
,...,x
p−
1
}
and
Right
=
{x
p
+1
,...,x
2
n−
1
,x
2
n
(=
b
)
}
as
showninFig.
5
so that
a ∈ Left
,
b ∈ Right
,
|Left∪{v, x
p
}|
=
p
,
|Right|
=2
n−p
,
C ∈{R, B, G}
and for every
,
2
|≤
2
,
n − p
2
|C ∩
(
Left ∪{v, x
p
}
)
|C ∩ Right|≤
.
Since
p
is even, by applying the inductive hypothesis to each of
Left∪{v, x
p
}
and
Right
, we can obtain the desired Perfect Matching.
x
v
x
1
=
v
1
=
x
2
n
=
b
x
2
=
a
x
3
x
4
x
6
x
p
x
p
x
5
Fig. 5.
A balanced partition and the desired Perfect Matching.









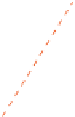


























































Search WWH ::

Custom Search