Geoscience Reference
In-Depth Information
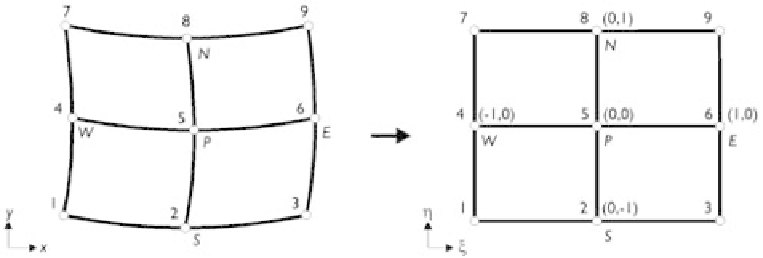
Figure 4.8
2-D local coordinate transformation.
and
k
=
1
ϕ
k
=
k
j
and satisfy
ϕ
k
(ξ
j
,
η
)
=
δ
1. They are written as
j
⎧
⎨
⎩
2
2
(ξξ
k
+
ξ
)(ηη
k
+
η
)/
4
k
=
1, 3, 7, 9
2
2
(ξξ
k
+
ξ
)(
1
−
η
)/
2
k
=
4, 6
ϕ
k
=
(4.84)
2
2
(
1
−
ξ
)(ηη
k
+
η
)/
2
k
=
2, 8
2
2
(
1
−
ξ
)(
1
−
η
)
k
=
5
Differentiating coordinate transformation (4.83) with respect to
ξ
and
η
leads to
∂
x
∂ξ
=
k
=
1
9
x
k
∂ϕ
k
∂ξ
,
∂
x
∂η
=
k
=
1
9
x
k
∂ϕ
k
∂η
,
(4.85)
k
=
1
k
=
1
∂
y
∂ξ
=
9
y
k
∂ϕ
k
∂ξ
∂
y
∂η
=
9
y
k
∂ϕ
k
∂η
,
,
and
9
9
9
2
x
∂ξ
2
2
x
∂ξ∂η
=
2
2
x
∂η
2
∂
x
k
∂
ϕ
k
∂ξ
∂
x
k
∂
ϕ
k
∂ξ∂η
,
∂
x
k
∂
ϕ
k
∂η
=
,
=
,
2
2
2
2
k
=
1
k
=
1
k
=
1
(4.86)
9
9
9
2
y
∂ξ
2
2
y
∂ξ∂η
=
2
2
y
∂η
2
∂
y
k
∂
ϕ
k
∂ξ
∂
y
k
∂
ϕ
k
∂ξ∂η
∂
y
k
∂
ϕ
k
∂η
=
,
,
=
.
2
2
2
2
k
=
1
k
=
1
k
=
1
The Jacobian determinant is Eq. (4.76). The first and second derivatives are given
by Eqs. (4.77), (4.78), and (4.80)-(4.82).
For a 3-D problem, the volume formed by twenty-seven points shown in Fig. 4.9
is adopted as the basic element. This irregular element is turned into a cube by the
following coordinate transformation between the physical domain (
x
,
y
,
z
) and the
logical domain (
ξ
,
η
,
ζ
):
27
27
27
x
=
x
k
ϕ
k
(ξ
,
η
,
ζ)
,
y
=
y
k
ϕ
k
(ξ
,
η
,
ζ)
,
z
=
z
k
ϕ
k
(ξ
,
η
,
ζ)
(4.87)
k
=
1
k
=
1
k
=
1