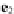Graphics Reference
In-Depth Information
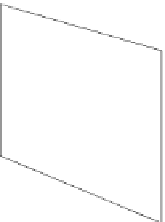
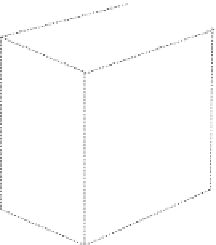
Fig. 6.5
The effect of
multiplying a vector by a
bivector
6.15 Duality
The ability to exchange pairs of geometric elements such as lines and planes in-
volves a
dual
operation, which in geometric algebra is relatively easy to define. For
example, given a multivector
A
its dual
A
∗
is defined as
A
∗
=
I
A
where
I
is the local pseudoscalar. For 2D this is
e
12
and for 3D it is
e
123
. Therefore,
given:
a
=
a
1
e
1
+
a
2
e
2
its dual is
a
∗
=
e
12
(a
1
e
1
+
a
2
e
2
)
=
a
1
e
121
+
a
2
e
122
=
a
2
e
1
−
a
1
e
2
which is another vector rotated 90° anticlockwise.
It is easy to show that
(
a
∗
)
∗
=−
a
, and two further dual operations return the
vector back to
a
.
In 3D the dual of a vector
e
1
is
e
123
e
1
=
e
23
which is the perpendicular bivector. Similarly, the dual of
e
2
is
e
31
and the dual of
e
3
is
e
12
.
For a general vector
a
1
e
1
+
a
2
e
2
+
a
3
e
3
its dual is
e
123
(a
1
e
1
+
e
1231
=
a
2
e
2
+
=
a
1
e
1231
+
a
2
e
1232
+
a
3
e
3
)
a
3
e
1233
=
a
3
e
12
+
a
1
e
23
+
a
2
e
31
.
The duals of the 3D basis bivectors are:
e
123
e
12
=
e
12312
=−
e
3
e
123
e
23
=
e
12323
=−
e
1
e
123
e
31
=
e
12331
=−
e
2
.