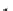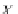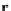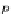Graphics Reference
In-Depth Information
Fig. 3.5
The normal vector
t
is derived from the cross
product
r
×
s
2
2
|
t
|=
+
2
2
+
1
2
=
3
2
3
i
2
3
j
1
3
k
.
t
u
=
+
+
3.14 Interpolating Vectors
In computer animation we need to vary quantities such as height, width, depth, light
intensity, radius, etc., such that they change over a sequence of animation frames.
The change may be linear or non-linear, and a variety of techniques exist for chang-
ing one numeric value into another. This process is called
interpolating
.
To interpolate between two values
v
1
and
v
2
we often use the linear interpolant:
v
tv
2
where the parameter
t
varies between 0 and 1. For example, given
v
1
=
=
(
1
−
t)v
1
+
2 and
v
2
=
10 we can compute a half-way point by making
t
=
0
.
5:
v
=
0
.
5
×
2
+
0
.
5
×
10
=
6
where
t
is linked to the animation frame number.
However, this technique cannot be used for changing quantities such as a light
source direction, dust-cloud particle velocity, or the direction and intensity of a
flame. This is because these quantities possess both magnitude and direction - they
are vector quantities.
For example, if we interpolated the
x
- and
y
-components of the vectors
T
[
]
23
T
, the in-between vectors would carry the change of orientation but ignore
the change in magnitude. To preserve both, we must design a spherical interpolant
that is sensitive to a vector's length
and
orientation.
Figure
3.6
shows two unit vectors
v
1
and
v
2
separated by an angle
θ
. The inter-
polated vector
v
can be defined as a portion of
v
1
and a portion of
v
2
:
v
and [4
7
]
b
v
2
.
Let's define the values of
a
and
b
such that they are a function of the separating
angle
θ
. Vector
v
is
tθ
from
v
1
and
(
1
=
a
v
1
+
−
t) θ
from
v
2
, and it is evident from Fig.
3.6
that using the sine rule
a
sin
(
1
b
sin
tθ
.
t) θ
=
(3.8)
−