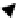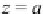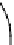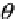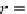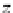Graphics Reference
In-Depth Information
Fig. 2.3
Polar representation
of a complex number
in Fig.
2.3
where we see the complex
number
z
=
a
+
bi
representing the oriented
line
r
. The length of
r
is obviously
√
a
2
b
2
, which is why the modulus of a com-
plex number has the same definition. We can see from Fig.
2.3
that the horizontal
component of
z
is
r
cos
θ
and the vertical component is
r
sin
θ
, which permits us to
write
+
z
=
a
+
bi
=
+
r
cos
θ
ri
sin
θ
=
r (
cos
θ
+
i
sin
θ) .
Note that
i
has been placed in front of the sin function.
The angle
θ
between
r
and the real axis is called the
argument
and written arg
(z)
,
and in this case
arg
(z)
=
θ.
One of Euler's discoveries concerns the relationship between the series for expo-
nential
e
, sin and cos:
e
iθ
=
cos
θ
+
i
sin
θ
which enables us to write
z
=
re
iθ
.
We are now in a position to revisit the product and quotient of two complex
numbers using polar representation. For example:
i
sin
θ)
w
=
s (
cos
φ
+
i
sin
φ)
zw
z
=
r (
cos
θ
+
=
+
+
rs (
cos
θ
i
sin
θ)(
cos
φ
i
sin
φ)
rs
cos
θ
cos
φ
i
2
sin
θ
sin
φ
=
+
i
cos
θ
sin
φ
+
i
sin
θ
cos
φ
+
=
rs
(
cos
θ
cos
φ
−
cos
θ
sin
φ)
sin
θ
sin
φ)
+
i (
sin
θ
cos
φ
+
and as