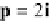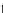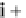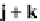Graphics Reference
In-Depth Information
Fig. 11.4
The vect
or
2
i
is
rotated 90° to
i
+
√
2
j
+
k
Let
θ
=
90°, therefore,
0
1
1
k
(
0
1
√
2
qp
=
+
√
2
i
+
+
2
i
)
2
√
2
(
−
=
1
+
j
).
Next, we post-multiply by
q
−
1
j
)
0
√
2
k
2
√
2
(
1
√
2
i
1
qpq
−
1
=
−
1
+
−
−
1
√
2
i
√
2
k
2
√
2
1
√
2
k
1
√
2
i
1
=
+
−
+
=
i
+
k
−
i
+
k
2
k
which confirms our prediction. Now let's show how this double angle arises.
We begin by defining a unit quaternion
q
:
q
=
v
and we will eventually assign values to
s
and
λ
. The vector
u
to be rotated is a pure
quaternion:
=
s
+
λ
ˆ
p
=
0
+
u
.
The inverse quaternion
q
−
1
is
q
−
1
=
s
−
λ
v
ˆ
therefore, the triple
qpq
−
1
is
qpq
−
1
=
+
ˆ
+
−
ˆ
(s
λ
v
)(
0
u
)(s
λ
v
)
=
(
−
λ
v
·
u
+
s
u
+
λ
v
×
u
)(s
−
λ
v
)
λ
2
(
ˆ
=−
λs
ˆ
v
·
u
+
λs
u
· ˆ
v
+
v
×
u
)
· ˆ
v
+
λ
2
(
ˆ
+
s
2
u
v
·
u
)
ˆ
v
+
λs
ˆ
v
×
u
−
λ
2
(
ˆ
−
λs
u
× ˆ
v
v
×
u
)
× ˆ
v
=
λ
2
(
ˆ
+
λ
2
(
ˆ
+
s
2
u
−
λ
2
(
ˆ
v
×
u
)
· ˆ
v
v
·
u
)
ˆ
v
+
2
λs
ˆ
v
×
u
v
×
u
)
× ˆ
v
.