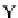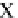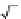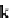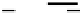Graphics Reference
In-Depth Information
Fig. 11.3
Rotating the vector
2
i
by the quaternion
q
=
cos
θ
+
sin
θ(
1
1
√
2
k
)
√
2
i
+
which, unfortunately, is not a pure
qu
aternion. It has not been rotated 45° and the
vector's magnitude is reduced to
√
3! Multiplying the vector by a non-orthogonal
quaternion seems to have converted some of the vector information into the quater-
nion's scalar component.
Not to worry. Could it be that an inverse quaternion reverses the operation? Let's
see what happens if we multiply this result, i.e.
qp
,by
q
−
1
.
Given
sin
θ
1
k
1
√
2
q
=
cos
θ
+
√
2
i
+
then
sin
θ
1
√
2
k
1
q
−
1
=
cos
θ
−
√
2
i
+
√
2
2
√
2
2
√
2
k
1
√
2
i
1
=
−
+
2
(
√
2
1
=
−
i
−
k
).
Therefore,
√
2
i
j
)(
√
2
1
2
(
−
qpq
−
1
=
1
+
+
−
i
−
k
)
√
2
(
√
2
i
√
2
(
√
2
i
√
2
j
2
−
k
1
=
−
+
j
)
·
(
−
i
−
k
)
+
(
i
+
k
)
+
+
j
)
−
i
+
+
√
2
√
2
√
2
j
√
2
j
1
2
(
=
−
+
+
i
+
k
+
2
i
+
−
i
+
+
k
)
√
2
j
=
+
+
i
k
which
is
a pure quaternion. Furthermore, its magnitude is 2, but what is strange, the
vector has been rotated 90° rather than 45° as shown in Fig.
11.4
.
If this 'sandwiching' of the vector by
q
and
q
−
1
is correct, it implies that increas-
ing
θ
to 90° should rotate
p
=
2
i
by 180° to 2
k
. Let's try this.