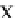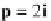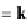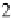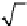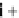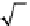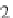Graphics Reference
In-Depth Information
Fig. 11.2
The vector 2
i
is
rotated 45° by the quaternion
q
=
cos
θ
+
sin
θ
k
and a pure quaternion to represent the vector 2
i
p
=
0
+
2
i
then
qp
=
2 cos
θ
i
+
sin
θ
k
×
2
i
.
With
θ
=
45° then
2
√
2
2
√
2
2
qp
=
i
+
k
×
2
i
√
2
i
√
2
j
=
+
which is a pure quaternion, i.e. a vector, and
p
has been rotated 45°.
Let's see what happens when
θ
=
180°:
qp
=
2 cos 180°
i
+
sin 180°
k
×
2
i
=−
2
i
which is also a pure quaternion, and
p
has been rotated 180°. Note that the vector has
not been scaled during the rotation. This is because we are using a unit quaternion.
Now let's see what happens when we reduce the angle between
v
and
p
.Let's
reduce the angle to 45° and retain the quaternion's magnitude at unity, as shown in
Fig.
11.3
. Therefore,
ˆ
1
√
2
i
1
√
2
k
v
ˆ
=
+
sin
θ
1
√
2
k
1
q
=
cos
θ
+
√
2
i
+
=
+
p
0
2
i
.
This time we must include the dot product term:
qp
=−
sin
θ
v
ˆ
·
u
+
cos
θ
u
+
sin
θ
v
ˆ
×
u
.
We let
θ
=
45°
√
2
2
√
2
2
√
2
2
1
√
2
k
1
√
2
k
1
√
2
1
√
2
qp
=−
i
+
·
(
2
i
)
+
2
i
+
i
+
×
2
i
√
2
i
=−
1
+
+
j