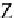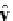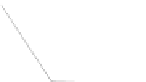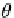Graphics Reference
In-Depth Information
Fig. 11.1
Three orthogonal
vectors
u
,
v
and
v
×
u
Hamilton had hoped that a quaternion could be used like a complex rotor, where
we saw in Chap. 2 that
R
θ
=
cos
θ
+
i
sin
θ
rotates a complex number by
θ
. Could the product of a quaternion
q
and a vector
u
rotate
u
about the quaternion's vector? Well yes, but only in a restricted sense. To
understand this, consider the scenario where we form the product of a unit quater-
nion
q
and a pure quaternion
p
. The unit quaternion
q
is defined as
q
=
s
+
λ
v
ˆ
where
s
2
λ
2
+
=
1
and the pure quaternion
p
encodes the vector
u
with a zero scalar term
p
=
0
+
u
.
In Chap. 5 we computed product
qp
, which in this context is
qp
=
(s
+
λ
v
)(
0
ˆ
+
u
)
=−
λ
v
ˆ
·
u
+
s
u
+
λ
v
ˆ
×
u
.
However, if
v
is orthogonal to
u
, the dot product term
ˆ
−
λ
v
ˆ
·
u
vanishes, and we are
left with
qp
=
s
u
+
λ
v
ˆ
×
u
.
Figure
11.1
illustrates this scenario, where
u
is perpendicular to
ˆ
v
, and
v
ˆ
×
u
is
perpendicular to the plane containing
u
and
v
.
ˆ
Now because
v
is a unit vector, the length of
ˆ
v
ˆ
×
u
is
|
u
|
, which means that we
have two orthogonal vectors, i.e.
u
and
v
ˆ
×
u
, with the same length. Therefore, to
rotate
u
about
v
, all that we have to do is to substitute cos
θ
for
s
and sin
θ
for
λ
:
ˆ
qp
=
cos
θ
u
+
sin
θ
v
ˆ
×
u
.
For example, if we create a quaternion whose vector is aligned with the
z
-axis as
shown in Fig.
11.2
with
q
=
cos
θ
+
sin
θ
k