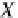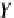Graphics Reference
In-Depth Information
Fig. 10.2
The point
P
remains fixed whilst the
frame
XYZ
is translated
(
−
t
x
,
−
t
y
,
−
t
z
)
For example, the origin of
XYZ
becomes
(t
x
,t
y
,t
z
)
in
X
Y
Z
:
⎡
⎣
⎤
⎦
=
⎡
⎣
⎤
⎦
⎡
⎣
⎤
⎦
t
x
t
y
t
z
1
100
t
x
010
t
y
001
t
z
000 1
0
0
0
1
.
Therefore, the transform for translating a frame by
(t
x
,t
y
,t
z
)
is
⎡
⎤
100
−
t
x
⎣
⎦
010
−
t
y
T
−
1
t
x
,t
y
,t
z
=
.
001
t
z
000 1
−
Now we consider rotated frames of reference in space.
10.3.2 Rotated Frames of Reference About Cartesian Axes
A 2D frame of reference can only be rotated within its plane, whereas a 3D frame
can be rotated about any axis, whether it be a Cartesian axis or some arbitrary axis.
Let's look at how
R
α,x
behaves when rotating frames about the
x
-axis, and apply
the results to the other axes.
We know that we can rotate a point,
α
about the
x
-axis using
⎡
⎤
10
0
⎣
⎦
.
R
α,x
=
0
cos
α
−
sin
α
0 n
α
cos
α
However,
R
α,x
can also be used to rotate a frame
−
α
about the
x
-axis. Similarly,
R
−
1
α,x
rotates a frame
α
about the same axis. Therefore, in general, we can use the
same technique for all three Cartesian axes.
Figure
10.3
(a) and (b) show our unit cube rotated by
90° about the
x
-axis,
whilst (c) and (d) show the frame rotated 90° about the same axis, with the cube
fixed.
−